Элементы квантовой статистики

179. Покажите, что при очень малом параметре вырождения распределения Бозе—Эйнштейна и Ферми—Дирака переходят в распределение Максвелла—Болыдмана.

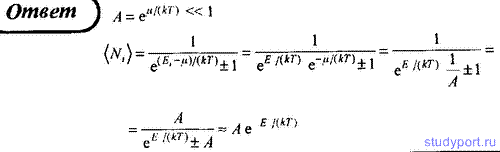
182. Объясните, при каких условиях можно применять статистику Максвелла—Больцмана к электронам в металле. Пользуясь распределением Ферми—Дирака, получите распределение Максвелла—Больцмана.

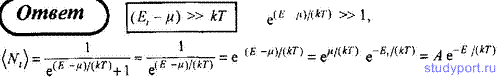
183. Определите функцию распределения для электронов, находящихся на энергетическом уровне E для случая E - E_F << kT, пользуясь: 1) статистикой Ферми — Дирака; 2) статистикой Максвелла — Больцмана.

184. Определите ф ... Читать дальше »

Элементы физики атомного ядра

7. Элементы физики атомного ядра и элементарных частиц

1. Определите массу нейтрального атома ⁵⁴₂₄Cr.

3. Определите, какую часть массы нейтрального атома ¹²₆C (m = 19,9272*10^-27 кг) составляет масса его электронной оболочки.

6. Определите, пользуясь таблицей Менделеева, число нейтронов и протонов в атомах платины и урана.

8. Определите плотность ядерного вещества, выражаемую числом нуклонов в 1 см³, если в ядре с массовым числ ... Читать дальше »

Элементы физики элементарных частиц

96. Известно, что в углеродно-азотном, или углеродном, цикле число ядер углерода остается неизменным. В результате этого цикла четыре ядра водорода ¹₁H (протона) превращаются в ядро гелия ⁴₂He, а также образуются три y-кванта, два позитрона и два нейтрино. Записав эту реакцию, определите выделяющуюся в этом процессе энергию.

100. Запишите схемы распада положительного и отрицательного мюонов.

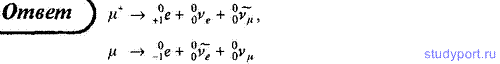
101. При соударении высокоэнергетического положительного мюона и электрона образуются два нейтрино. Запишите эту реакцию и объясните, какой тип нейтрино образуется.

... Читать дальше »

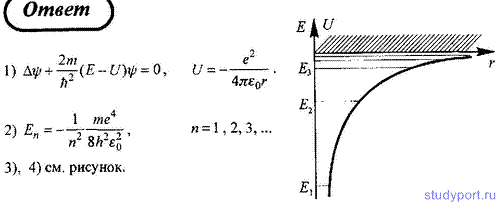
128. Представьте: 1) уравнение Шредингера для стационарных состояний электрона, находящегося в атоме водорода; 2) собственные значения энергии, удовлетворяющие уравнению; 3) график потенциальной энергии взаимодействия электрона с ядром; 4) возможные дискретные значения энергии на этом графике.

 

130. Волновая функция ψ_nlml (r,ν,φ), описывающая атом водорода, определяется главным квантовым числом n, орбитальным квантовым числом l и магнитным квантовым числом m_l. Определите, чему равно число различных состояний, соответствующих данному n.

131. Запишите возможные значения орбитального квантового числа l и магнитного квантового числа m_l для главного квантового числа n = 4.

... Читать дальше »

38. Определите импульс и энергию: 1) рентгеновского фотона; 2) электрона, если длина волны того и другого равна 10¹⁰ м.

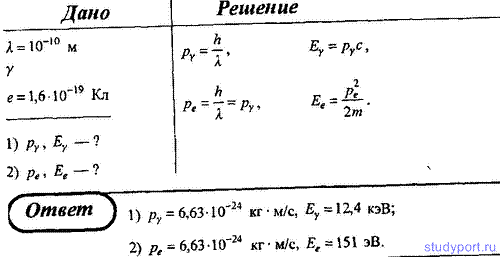
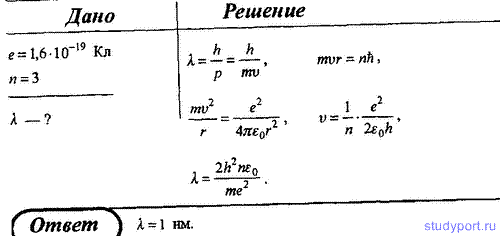
39. Определите длину волны де Бройля для электрона, находящегося в атоме водорода на третьей боровской орбите.

40. Определите длину волны де Бройля для нейтрона, движущегося со средней квадратичной скоростью при T = 290 К.

41. Протон движется в однородном магнитном поле с индукцией B = 15 мТл по окружности радиусом R = 1,4 м. Определите длину волны де Бройля для протона.

42. Определите, какую ускоряющую разность потенциа ... Читать дальше »

1. Определите энергию фотона, испускаемого при переходе электрона в атоме водорода с третьего энергетического уровня на второй.

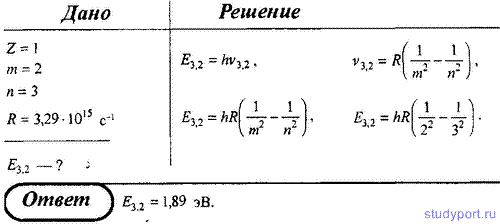
2. Определите максимальную и минимальную энергии фотона в видимой серии спектра водорода (серии Бальмера).

3. Определите длину волны λ, соответствующую второй спектральной линии в серии Пашена.

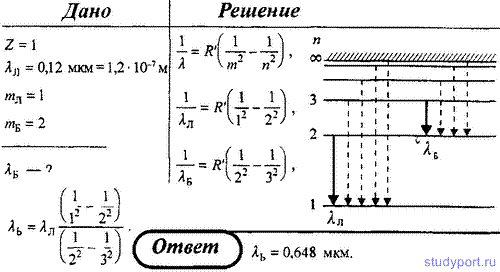
4. Максимальная длина волны спектральной водородной линии серии Лаймана равна 0,12 мкм. Предполагая, что постоянная Ридберга неизвестна, определите максимальную длину волны линии серии Бальмера.

< ... Читать дальше »

Квантовая природа излучения

173. Определите, во сколько раз необходимо уменьшить термодинамическую температуру черного тела, чтобы его энергетическая светимость Re ослабилась в 16 раз.

 

174. Температура внутренней поверхности муфельной печи при открытом отверстии площадью 30 см² равна 1,3 кК. Принимая, что отверстие печи излучает как черное тело, определите, какая часть мощности рассеивается стенками, если потребляемая печью мощность составляет 1,5 кВт.

175. Энергетическая светимость черного тела R_e = 10 кВт/м². Определите длину волны, соответствующую максимуму спектральной плотности энергетической светимости этог ... Читать дальше »

139. Определите степень поляризации частично поляризованного света, если амплитуда светового вектора, соответствующая максимальной интенсивности света, в 3 раза больше амплитуды, соответствующей его минимальной интенсивности.

140. Степень поляризации частично поляризованного света составляет 0,75. Определите отношение максимальной интенсивности света, пропускаемого анализатором, к минимальной.

141. Определите степень поляризации p света, который представляет собой смесь естественного света с плоскополяризованным, если интенсивность поляризованного света равна интенсивности естественного.

142. Определите степень поляризации p света, к ... Читать дальше »

113. Докажите, что если монохроматический пучок света падает на грань призмы с показателем преломления n под малым углом, то при малом преломляющем угле A призмы угол отклонения φ лучей не зависит от угла падения и равен A(n-1).

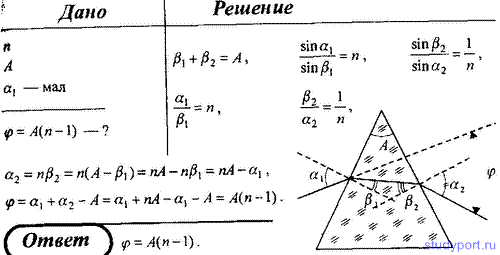
114. На стеклянную призму с преломляющим углом A = 55° падает луч света под углом α₁ = 30°. Определите угол отклонения φ луча призмой, если показатель преломления n стекла равен 1,5.

115. На грань стеклянной призмы (n = 1,5) нормально падает луч света. Определите угол отклонения φ луча призмой, если ее преломляющий угол A = 30°.

116. На рисунке ... Читать дальше »

68. Точечный источник света (λ = 0,5 мкм) расположен на расстоянии a = 1 м перед диафрагмой с круглым отверстием диаметра d = 2 мм. Определите расстояние b от диафрагмы до точки наблюдения, если отверстие открывает три зоны Френеля.

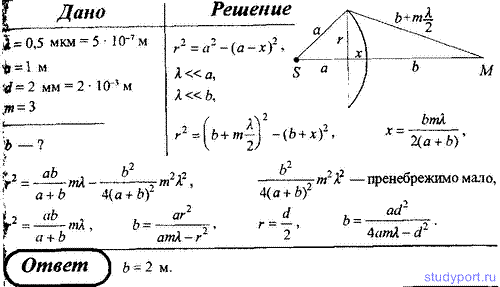
69. Определите радиус третьей зоны Френеля, если расстояние от точечного источника света (λ = 0,6 мкм) до волновой поверхности и от волновой поверхности до точки наблюдения равно 1,5 м.

70. На диафрагму с круглым отверстием диаметром d = 5 мм падает нормально параллельный пучок света с длиной волны λ = 0,6 мкм. Определите расстояние от точки наблюдения до отверстия, если отверстие открывает: 1) две зоны Френеля; 2) три зоны Френеля.

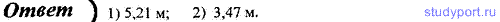
71. Опр ... Читать дальше »

41. Определите длину отрезка l₁, на котором укладывается столько же длин волн монохроматического света в вакууме, сколько их укладывается на отрезке l₂ = 5 мм в стекле. Показатель преломления стекла n = 1,5.

 

42. Два параллельных световых пучка, отстоящих друг от друга на расстоянии d = 5 см, падают на кварцевую призму (n = 1,49) с преломляющим углом α = 25° . Определите оптическую разность хода d этих пучков на выходе их из призмы.

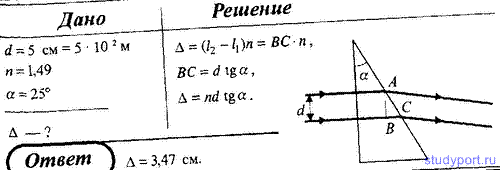
43. В опыте Юнга расстояние между щелями d = 1 мм, а расстояние l от щелей до экрана равно 3 м. Определите: 1) положение первой светлой полосы; 2) положение третьей темной полосы, если щели освещать монохроматическим светом с длиной волны λ = 0,5 мкм.

... Читать дальше »

 Оптика. Квантовая природа излучения

 

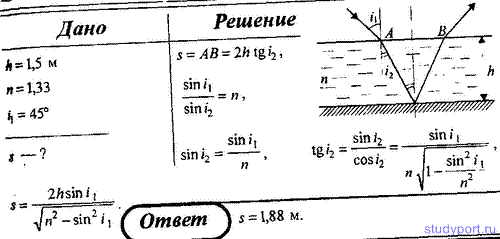
1. На горизонтальном дне бассейна глубиной h = 1,5 м лежит плоское зеркало. Луч света входит в воду под углом i₁ = 45°. Определите расстояние s от места вхождения луча в воду до места выхода его на поверхность воды после отражения от зеркала. Показатель преломления воды n = 1,33.

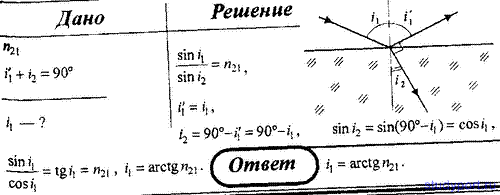
2. Луч света падает на плоскую границу раздела двух сред, частично отражается и частично преломляется. Определите угол падения, при котором отраженный луч перпендикулярен преломленному лучу.

3. На плоскопараллельную стеклянную (n = 1,5) пластинку толщиной d = 5 см падает под углом i = 30° луч света. Определите боковое смещение луча, прошедшего сквозь эту пластинку.

... Читать дальше »

Электромагнитные волны

157. Скорость распространения электромагнитных волн в некоторой среде составляет v = 250 Мм/с. Определите длину волны электромагнитных волн в этой среде, если их частота в вакууме ν₀ = 1 МГц.

158. Для демонстрации преломления электромагнитных волн Герц применял призму, изготовленную из парафина. Определите показатель преломления парафина, если его диэлектрическая проницаемость ε = 2 и магнитная проницаемость μ = 1.

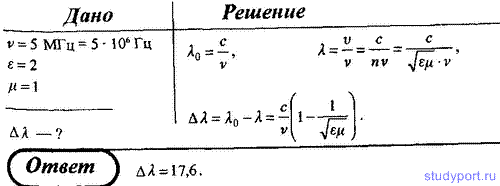
159. Электромагнитная волна с частотой ν = 5 МГц переходит из немагнитной среды c диэлектрической проницаемостью ε = 2 б вакуум. Определите приращение ее длины волны.

... Читать дальше »

1. Гармонические колебания величины s описываются уравнением s = 0,02 cos (6πt + π/3), м. Определите: 1) амплитуду колебаний; 2) циклическую частоту; 3) частоту колебаний; 4) период колебаний.

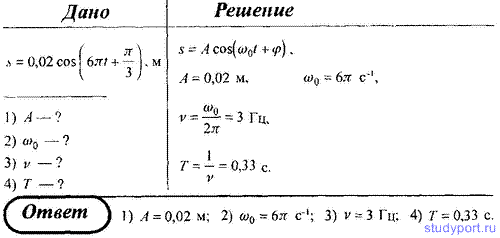
2. Запишите уравнение гармонического колебательного движения точки, совершающей колебания с амплитудой A = 8 см, если за t = 1 мин совершается n = 120 колебаний и начальная фаза колебаний равна 45°.

3. Материальная точка совершает гармонические колебания с амплитудой A = 4 см и периодом T = 2 с. Напишите уравнение движения точки, если ее движение начинается из положения x₀ = 2 см.

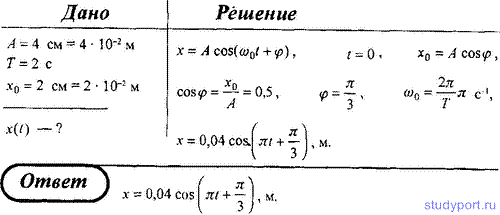
4. Точка совершает г ... Читать дальше »

Основы теории Максвелла для электромагнитного поля

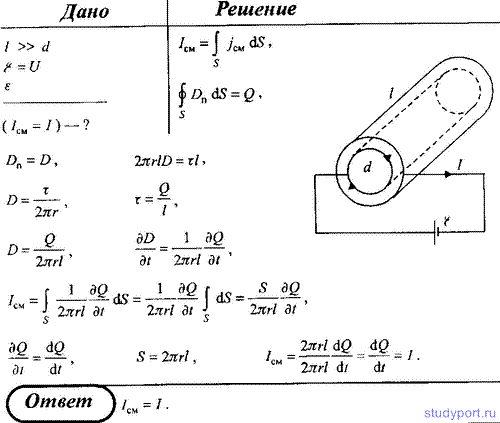
230. Длинный цилиндрический конденсатор заряжается от источника ЭДС. Пренебрегая краевыми эффектами, докажите, что ток смещения в диэлектрике, заполняющем пространство между обкладками конденсатора, равен току в цепи источника ЭДС.

234. Докажите с помощью одного из уравнений Максвелла, что переменное во времени магнитное поле не может существовать без электрического поля.

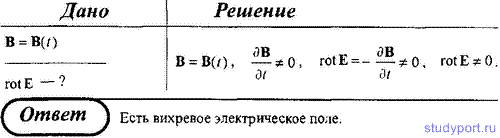
235. Докажите, что уравнения Максвелла rotE = -δB/dt и divB = 0 совместимы, т. е. первое из них не противоречит второму.

236. Ток, проходящий по обмотке длинного прямог ... Читать дальше »

116. Определите разность фаз Δφ колебаний двух точек, лежащих на луче и друг от друга на расстоянии Δl = 1 м, если длина волны λ = 0,5 м.

 

117. Две точки лежат на луче и находятся от источника колебаний на расстоянии x₁ = 4 м и x₂ = 7 м. Период колебаний T = 20 мс и скорость v распространения волны равна 300 м/с. Определите разность фаз колебаний этих точек.

118. Волна распространяется в упругой среде со скоростью v = 150 м/с. Определите частоту ν колебаний, если минимальное расстояние Δx между точками среды, фазы колебаний которых противоположны, равно 0,75 м.

119. Определите длину волны λ, если числовое значение волнового вектора k равно 0,02512 см^{-1 ... Читать дальше »}