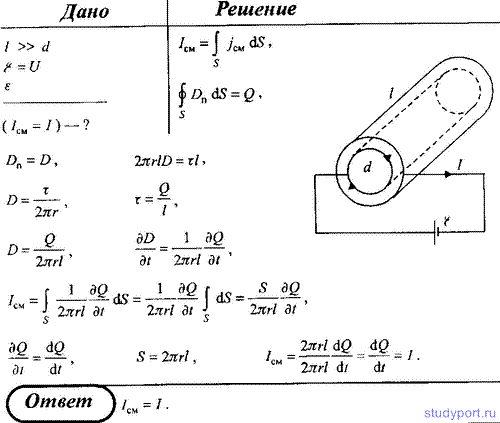
230. Длинный цилиндрический конденсатор заряжается от источника ЭДС. Пренебрегая краевыми эффектами, докажите, что ток смещения в диэлектрике, заполняющем пространство между обкладками конденсатора, равен току в цепи источника ЭДС.

234. Докажите с помощью одного из уравнений Максвелла, что переменное во времени магнитное поле не может существовать без электрического поля.

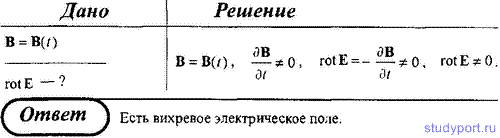
235. Докажите, что уравнения Максвелла rotE = -δB/dt и divB = 0 совместимы, т. е. первое из них не противоречит второму.

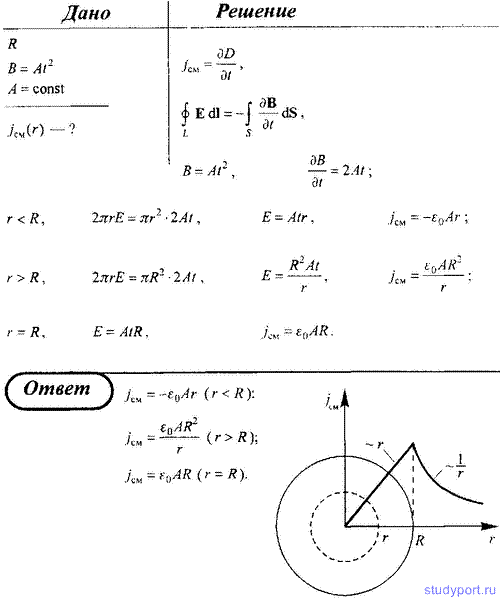
236. Ток, проходящий по обмотке длинного прямого соленоида радиусом изменяют так, что магнитное поле внутри соленоида растет со временем по закону В = At², где А — некоторая постоянная. Определите плотность тока смещения как функцию расстояния r от оси соленоида. Постройте график зависимости j_см(r).

237. В физике известно так называемое уравнение непрерывности, выражающее закон сохранения заряда. Докажите, что уравнения Максвелла содержат это уравнение. Выведите дифференциальную форму уравнения непрерывности.

238. Определите силу тока смещения между квадратными пластинами конденсатора со стороной 5 см, если напряженность электрического поля изменяется со скоростью 4,52 МВ/(м*с).