1. Гармонические колебания величины s описываются уравнением s = 0,02 cos (6πt + π/3), м. Определите: 1) амплитуду колебаний; 2) циклическую частоту; 3) частоту колебаний; 4) период колебаний.

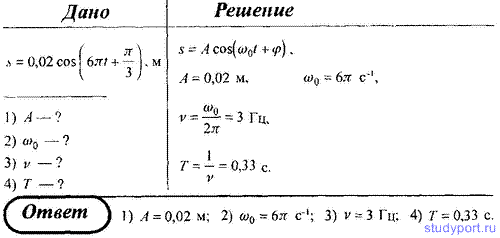
2. Запишите уравнение гармонического колебательного движения точки, совершающей колебания с амплитудой A = 8 см, если за t = 1 мин совершается n = 120 колебаний и начальная фаза колебаний равна 45°.

3. Материальная точка совершает гармонические колебания с амплитудой A = 4 см и периодом T = 2 с. Напишите уравнение движения точки, если ее движение начинается из положения x₀ = 2 см.

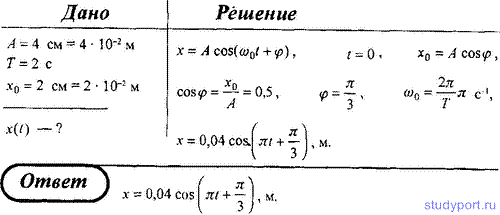
4. Точка совершает гармонические колебания с периодом T = 6 с и начальной фазой, равной нулю. Определите, за какое время, считая от начала движения, точка сместится от положения равновесия на половину амплитуды.

5. Напишите уравнение гармонического колебания точки, если его амплитуда A = 15 см, максимальная скорость колеблющейся точки v_max = 30 см/с, начальная фаза φ = 10°.

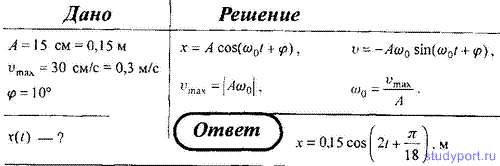
6. Точка совершает гармонические колебания по закону x = 3 cos (πt/2 + π/8), м. Определите: 1) период T колебаний: 2) максимальную скорость V_max точки; 3) максимальное ускорение a_max точки.

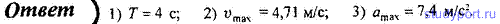
7. Точка совершает гармонические колебания с амплитудой A = 10 см и периодом T = 5 с. Определите для точки: 1) максимальную скорость; 2) максимальное ускорение.

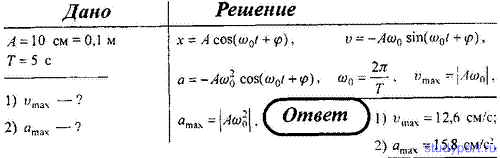
8. Скорость материальной точки, совершающей гармонические колебания, задается уравнением v(t) = -6 sin 2 πt, м/с. Запишите зависимость смещения этой точки от времени.

9. Материальная точка совершает колебания согласно уравнению x = A sin ωt. В какой-то момент времени смещение точки x₁ = 15 см. При возрастании фазы колебания в два раза смещение x₂ оказалось равным 24 см. Определите амплитуду A колебания.

10. Материальная точка совершает гармонические колебания согласно уравнению x = 0,02 cos (πt + π/2), м. Определите: 1) амплитуду колебаний; 2) период колебаний; 3) начальную фазу колебаний; 4) максимальную скорость точки; 5) максимальное ускорение точки; 6) через сколько времени после начала отсчета точка будет проходить через положение равновесия.

11. Определите максимальные значения скорости и ускорения точки, совершающей гармонические колебания с амплитудой A = 3 см и периодом T = 4 с.

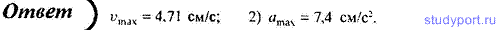
12. Материальная точка, совершающая гармонические колебания с частотой ν = 1 Гц, в момент времени t = 0 проходит положение, определяемое координатой х₀ = 5 см, со скоростью v₀ = -15 см/с. Определите амплитуду колебаний.

13. Тело массой m = 10 г совершает гармонические колебания по закону х = 0,1 cos(4πt + π/4), м. Определите максимальные значения: 1) возвращающей силы; 2) кинетической энергии.

14. Материальная точка массой m = 50 г совершает гармонические колебания согласно уравнению x = 0,1 cos 3πt/2, м. Определите: 1) возвращающую силу F для момента времени t = 0,5 с; 2) полную энергию Е точки.

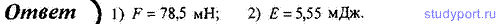
15. Материальная точка массой m = 20 г совершает гармонические колебания по закону x = 0,1 cos(4πt + π/4), м. Определите полную энергию Е этой точки.

16. Полная энергия E гармонически колеблющейся точки равна 10 мкДж, а максимальная сила F_max, действующая на точку, равна -0,5 мН. Напишите уравнение движения этой точки, если период T колебаний равен 4 с, а начальная фаза φ = π/6.

17. Определите отношение кинетической энергии T точки, совершающей гармонические колебания, к ее потенциальной энергии П, если известна фаза колебания.

18. Определите полную энергию материальной точки массой m, колеблющейся по закону x = A cos(ω₀t + φ).

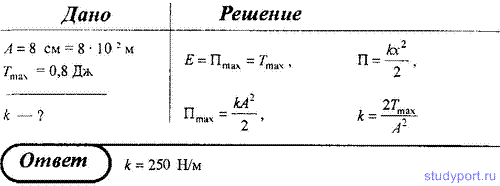
19. Груз, подвешенный к спиральной пружине, колеблется по вертикали с амплитудой A = 8 см. Определите жесткость k пружины, если известно, что максимальная кинетическая энергия T_max груза составляет 0,8 Дж.

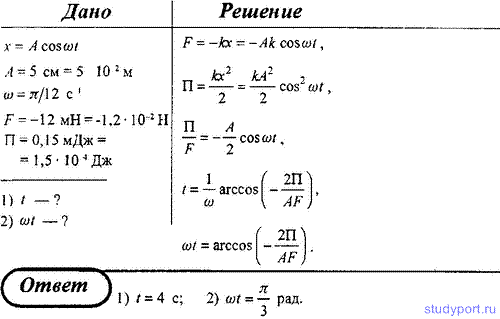
20. Материальная точка колеблется согласно уравнению х = A cos ωt, где A = 5 см и ω = π/12 с^-1. Когда возвращающая сила F в первый раз достигает значения -12 мН, потенциальная энергия П точки оказывается равной 0,15 мДж. Определите: 1) этот момент времени t; 2) соответствующую этому моменту фазу ωt.

21. Груз, подвешенный к спиральной пружине, колеблется по вертикали с амплитудой A = 6 см. Определите полную энергию E колебаний груза, если жесткость k пружины составляет 500 Н/м.

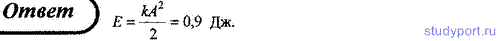
22. Спиральная пружина обладает жесткостью k = 25 Н/м. Определите, тело какой массой m должно быть подвешено к пружине, чтобы за t = 1 мин совершалось 25 колебаний.

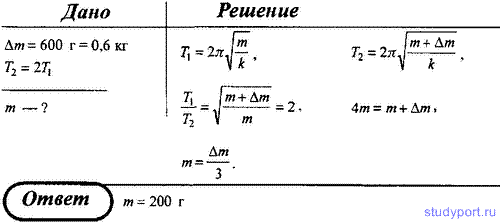
23. Если увеличить массу груза, подвешенного к спиральной пружине, на 600 г, то период колебаний груза возрастает в 2 раза. Определите массу первоначально подвешенного груза.

24. При подвешивании грузов массами m₁ = 600 г и m₂ = 400 г к свободным пружинам последние удлинились одинаково (l = 10 см). Пренебрегая массой пружин, определите: 1) периоды колебаний грузов; 2) какой из грузов при одинаковых амплитудах обладает большей энергией и во сколько раз.

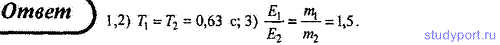
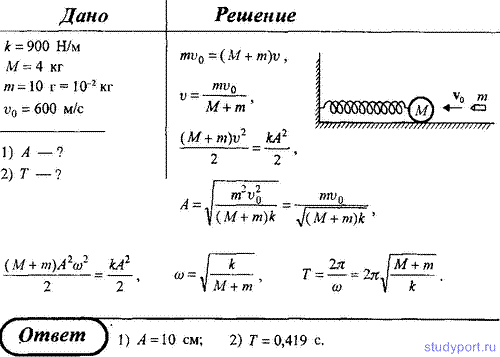
25. На горизонтальной пружине жесткостью k = 900 Н/м укреплен шар массой M = 4 кг, лежащий на гладком столе, по которому он может скользить без трения. Пуля массой m = 10 г, летящая с горизонтальной скоростью v₀ = 600 м/с и имеющая в момент удара скорость, направленную вдоль оси пружины, попала в шар и застряла в нем. Пренебрегая массой пружины и сопротивлением воздуха, определите: 1) амплитуду колебаний шара; 2) период колебаний шара.

26. На чашку весов массой M, подвешенную на пружине жесткостью k, с высоты h падает небольшой груз массой m. Удар груза о дно чашки является абсолютно неупругим. Чашка в результате падения груза начинает совершать колебания. Определите амплитуду A этих колебаний.

27. Физический маятник представляет собой тонкий однородный стержень длиной 35 см. Определите, на каком расстоянии от центра масс должна быть точка подвеса, чтобы частота колебаний была максимальной.

28. Однородный диск радиусом R = 20 см колеблется около горизонтальной оси, проходящей на расстоянии l = 15 см от центра диска. Определите период T колебаний диска относительно этой оси.

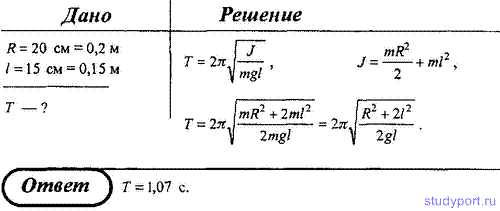
29. Тонкий обруч радиусом R = 50 см подвешен на вбитый в стену гвоздь и колеблется в плоскости, параллельной стене. Определите период T колебаний обруча.

30. Тонкий однородный стержень длиной l = 60 см может свободно вращаться вокруг горизонтальной оси, проходящей через верхний конец стержня. Стержень отклонили на угол α₀ = 0,01 рад и в момент времени t₀ = 0 отпустили. Считая колебания малыми, определите период колебаний стержня и запишите функцию α(t).

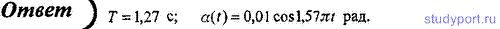
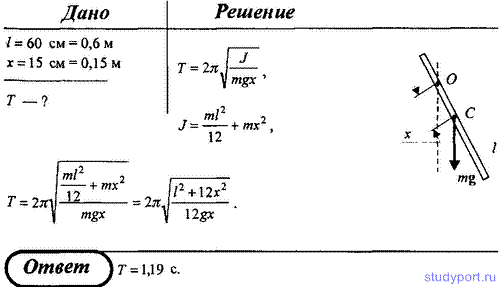
31. Тонкий однородный стержень длиной l = 60 см может свободно вращаться вокруг горизонтальной оси, отстоящей на расстоянии x = 15 см от его середины. Определите период колебаний стержня, если он совершает малые колебания.

32. Маятник состоит из стержня (l = 30 см, m = 50 г), на верхнем конце которого укреплен маленький шарик (материальная точка массой m' = 40 г), на нижнем — шарик (R = 5 см, M = 100 г). Определите период колебания этого маятника около горизонтальной оси, проходящей через точку О в центре стержня.

33. Математический маятник, состоящий из нити длиной l = 1 м и свинцового шарика радиусом r = 2 см, совершает гармонические колебания с амплитудой A = 6 см. Определите: 1) скорость шарика при прохождении им положения равновесия; 2) максимальное значение возвращающей силы. Плотность свинца ρ = 11,3 г/см³.

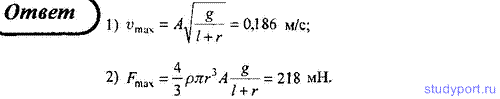
34. Два математических маятника имеют одинаковую массу, длину, отличающиеся в n = 1,5 раза, и колеблются с одинаковой угловой амплитудой. Определите, какой маятник обладает большей энергией и во сколько раз.

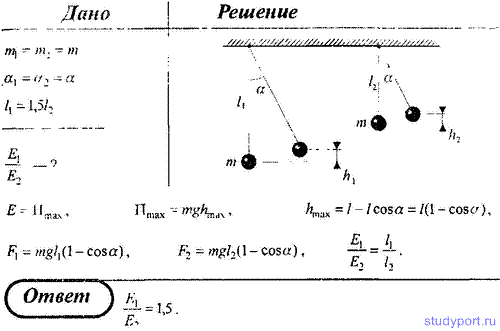
35. Два математических маятника, длины которых отличаются на Δl = 16 см, совершают за одно и то же время один n₁ = 10 колебаний, другой — n₂ = 6 колебаний. Определите длины маятников l₁ и l₂.

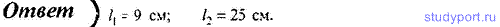
36. Математический маятник длиной l = 50 см подвешен в кабине самолета. Определите период T колебаний маятника, если самолет движется: 1) равномерно; 2) горизонтально с ускорением a = 2,5 м/с².

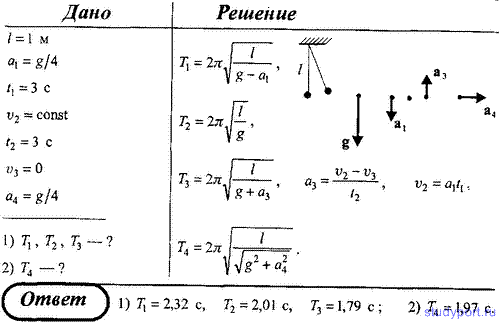
37. Математический маятник длиной l = 1 м подвешен к потолку кабины, которая начинает опускаться вертикально вниз с ускорением a₁ = g/4. Спустя время t₁ = 3 с после начала движения кабина начинает двигаться равномерно, а затем в течение 3 с тормозится до остановки. Определите: 1) периоды T₁, T₂, T₃ гармонических колебаний маятника на каждом из участников пути; 2) период T₄ гармонических колебаний маятника при движении точки подвеса в горизонтальном направлении с ускорением a₄ = g/4.

38. Колебательный контур состоит из катушки индуктивностью L = 1 мГн и конденсатора емкостью C = 2 нФ. Пренебрегая сопротивлением контура, определите, на какую длину волны этот контур настроен.

39. Колебательный контур состоит из катушки индуктивностью L = 0,2 мГн и конденсатора площадью пластин S = 155 см², расстояние между которыми d = 1,5 мм. Зная, что контур резонирует на длину волны λ = 630 м, определите диэлектрическую проницаемость среды, заполняющей пространство между пластинами конденсатора.

40. Колебательный контур содержит соленоид (длина l = 5 см, площадь поперечного сечения S₁ = 1,5 см², число витков N = 500) и плоский конденсатор (расстояние между пластинами d = 1,5 мм, площадь пластин S₂ = 100 см²). Определите частоту ω₀ собственных колебаний контура.

41. Колебательный контур состоит из катушки индуктивностью L = 0,1 Гн и конденсатора емкостью C = 39,5 мкФ. Заряд конденсатора Q_m = 3 мкКл. Пренебрегая сопротивлением контура, запишите уравнение: 1) изменения силы тока в цепи в зависимости от времени; 2) изменения напряжения на конденсаторе в зависимости от времени.

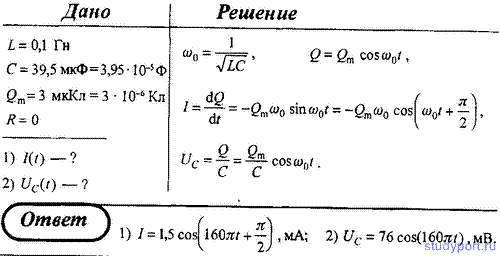
42. Сила тока в колебательном контуре, содержащем катушку индуктивностью L = 0,1 Гн и конденсатор, со временем изменяется согласно уравнению I = - 0,1 sin 200πt, А. Определите: 1) период колебаний; 2) емкость конденсатора; 3) максимальное напряжение на обкладках конденсатора; 4) максимальную энергию магнитного поля; 5) максимальную энергию электрического поля.

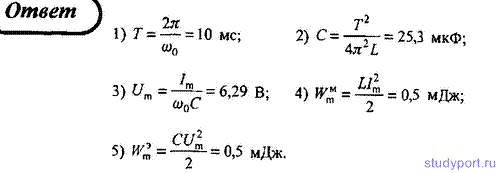
43. Энергия свободных незатухающих колебаний, происходящих в колебательном контуре, составляет 0,2 мДж. При медленном раздвигании пластин конденсатора частота колебаний увеличилась в n = 2 раза. Определите работу, совершенную против сил электрического поля.

44. Конденсатор емкостью С зарядили до напряжения U_m и замкнули на катушку индуктивностью L. Пренебрегая сопротивлением контура, определите амплитудное значение силы тока в данном колебательном контуре.

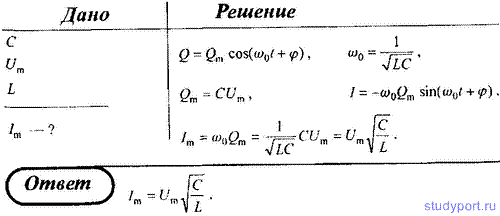
45. Колебательный контур содержит катушку с общим числом витков N = 100 индуктивностью L = 10 мкГн и конденсатор емкостью C = 1 нФ. Максимальное напряжение U_m на обкладках конденсатора составляет 100 В. Определите максимальный магнитный поток, пронизывающий катушку.

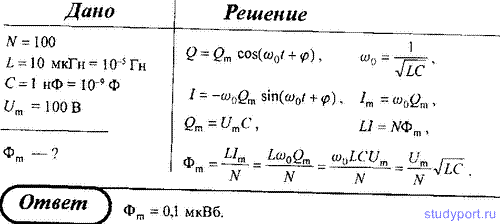
46. Два одинаково направленных гармонических колебания одинакового периода с амплитудами A₁ = 4 см и A₂ = 8 см имеют разность фаз φ = 45° . Определите амплитуду результирующего колебания.

47. Амплитуда результирующего колебания, получающегося при сложении двух одинаково направленных гармонических колебаний одинаковой частоты, обладающих разностью фаз 60°, равна A = 6 см. Определите амплитуду A₂ второго колебания, если A₁ = 5 см.

48. Определите разность фаз двух одинаково направленных гармонических колебаний одинаковой частоты и амплитуды, если амплитуда их результирующего колебания равна амплитудам складываемых колебаний.

49. Разность фаз двух одинаково направленных гармонических колебаний одинакового периода T = 4 с и одинаковой амплитуды A = 5 см составляет π/4. Напишите уравнение движения, получающегося в результате сложения этих колебаний, если начальная фаза одного из них равна нулю.

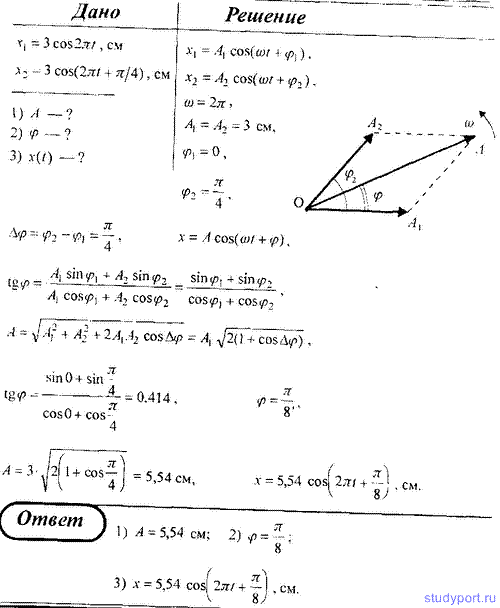
50. Складываются два гармонических колебания одного направления, описываемых уравнениями x₁ = 3 cos 2πt, см и x₂ = 3 cos (2πt + π/4), см. Определите для результирующего колебания: 1) амплитуду; 2) начальную фазу. Запишите уравнение результирующего колебания и представьте векторную диаграмму сложения амплитуд.

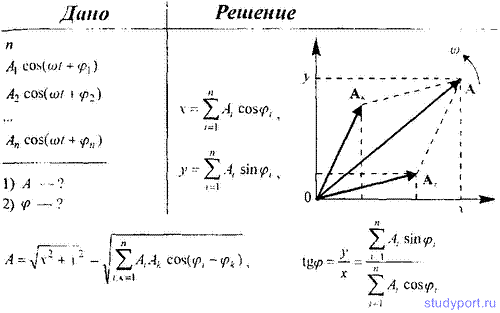
51. Точка одновременно участвует в n одинаково направленных гармонических колебаниях одинаковой частоты: A₁ cos(ωt + φ₁), A₂ cos(ωt + φ₂),A_n cos(ωt)/ + φ_n). Используя метод вращающегося вектора амплитуды, определите для результирующего колебания: 1) амплитуду; 2) начальную фазу.

52. Частоты колебаний двух одновременно звучащих камертонов строены на 560 и 560,5 Гц. Определите период биений.

53. В результате сложения двух колебаний, период одного из которых T₁ = 0,02 с. получают биения с периодом T₆ = 0,2 с. Определите период T₂ второго складываемого колебания.

54. Складываются два гармонических колебания одного направления, имеющие одинаковые амплитуды и одинаковые начальные фазы, с периодами T₁ = 2 с и T₂ = 2,05 с. Определите: 1) период результирующего колебания; 2) период биения.

55. Результирующее колебание, получающееся при сложении двух гармонических колебаний одного направления, описывается уравнением вида x = A cost cos45t (t —в секундах). Определите: 1) циклические частоты складываемых колебаний; 2) период биений результирующего колебания.

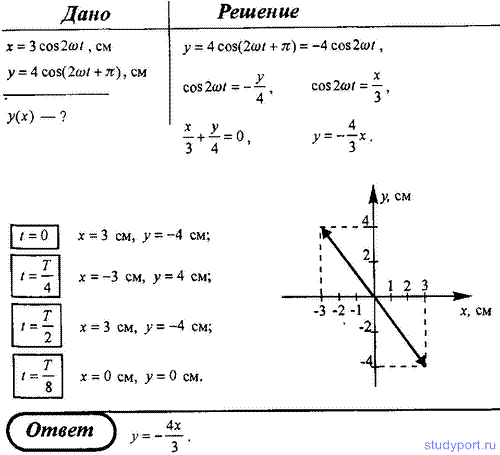
56. Точка участвует одновременно в двух гармонических колебаниях, происходящих во взаимно перпендикулярных направлениях и описываемых уравнениями x = 3 cos ωt, см и y = 4 cos ωt, см. Определите уравнение траектории точки и вычертите ее с нанесением масштаба.

57. Точка участвует одновременно в двух гармонических колебаниях, происходящих во взаимно перпендикулярных направлениях и описываемых уравнениями x = 3 cos 2ωt, см и y = 4 cos(2ωt + п), см. Определите уравнение траектории точки и вычертите ее с нанесением масштаба.

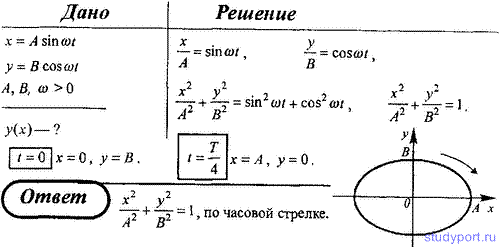
58. Точка участвует одновременно в двух гармонических колебаниях, происходящих во взаимно перпендикулярных направлениях и описываемых уравнениями x = A sin ωt и y = В cos ωt, где A, B и ω — положительные постоянные. Определите уравнение траектории точки, вычертите ее с нанесением масштаба, указав направление ее движения по этой траектории.

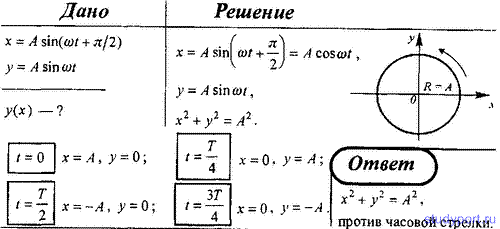
59. Точка участвует одновременно в двух гармонических колебаниях одинаковой частоты, происходящих во взаимно перпендикулярных направлениях и описываемых уравнениями x = A sin(ωt + π/2) и y = A sin πt. Определите уравнение траектории точки и вычертите ее с нанесением масштаба, указав направление ее движения по этой траектории.

60. Точка участвует в двух гармонических колебаниях, происходящих во взаимно перпендикулярных направлениях и описываемых уравнениями х = cos 2π/ и y = cos πt. Определите уравнение траектории точки и вычертите ее с нанесением масштаба.

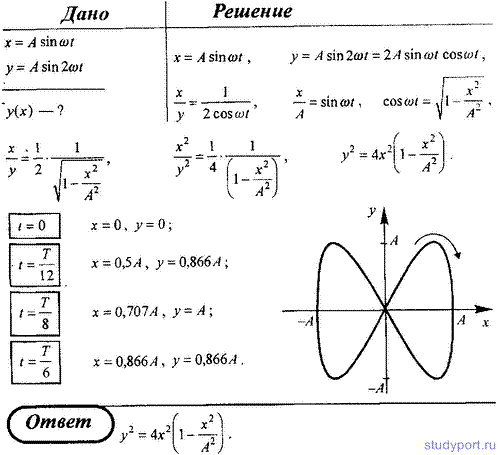
61. Точка участвует одновременно в двух гармонических колебаниях, происходящих во взаимно перпендикулярных направлениях и описываемых уравнениями x = A sin ωt и y = A sin 2ωt. Определите уравнение траектории точки и вычертите ее с нанесением масштаба.

62. Период затухающих колебаний T = 1 с, логарифмический декремент затухания Θ = 0,3, начальная фаза равна нулю. Смещение точки при t = 2Т составляет 5 см. Запишите уравнение движения этого колебания.

64. Амплитуда затухающих колебаний маятника за t = 2 мин уменьшилась в 2 раза. Определите коэффициент затухания δ.

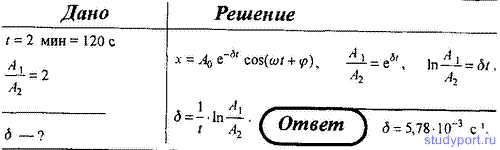
65. Логарифмический декремент колебаний Θ маятника равен 0,01. Определите число N полных колебаний маятника до уменьшения его амплитуды в 3 раза.

66. Амплитуда затухающих колебаний математического маятника за 1 мин уменьшилась в 3 раза. Определите, во сколько раз она уменьшится за 4 мин.

67. Начальная амплитуда затухающих колебаний маятника A₀ = 3 см. По истечении t₁ = 10 с A₁ = 1 см. Определите, через сколько времени амплитуда колебаний станет равной A₂ = 0,3 см.

68. Тело массой m = 0,6 кг, подвешенное к спиральной пружине жесткостью k = 30 Н/м, совершает в некоторой среде упругие колебания. Логарифмический декремент колебаний Θ = 0,01. Определите: 1) время, за которое амплитуда колебаний уменьшится в 3 раза; 2) число полных колебаний, которые должна совершить гиря, чтобы произошло подобное уменьшение амплитуды.

69. Докажите, что выражения для коэффициента затухания δ = r/(2m) и циклической частоты ω = корень(ω₀² - δ²)=корень(k/m - (r/2m)²) > 0 следуют из решения дифференциального уравнения для затухающих колебаний mx + rx + kx=0 (m — масса тела, r — коэффициент сопротивления, k — коэффициент упругости).

70. При наблюдении затухающих колебаний выяснилось, что для двух последовательных колебаний амплитуда второго меньше амплитуды первого на 60%. Период затухающих колебаний T = 0,5 с. Определите: 1) коэффициент затухания δ; 2) для тех же условий частоту ν₀ незатухающих колебаний.

71. Тело массой m = 100 г, совершая затухающие колебания, за t = 1 мин потеряло 40% своей энергии. Определите коэффициент сопротивления r.

72. Дифференциальное уравнение для заряда в электрическом колебательном контуре задается в виде L(d²Q/dt²) + R (dQ/dt) +Q/C = 0. Найдите решение этого уравнения. Определите: 1) собственную частоту контура; 2) циклическую частоту ω; 3) коэффициент затухания δ.

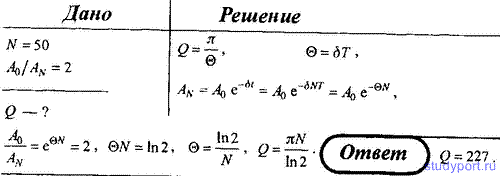
73. За время, в течение которого система совершает N = 50 полных колебаний, амплитуда уменьшается в 2 раза. Определите добротность Q системы.

74. Частота свободных затухающих колебаний некоторой системы ω = 65 рад/с, а ее добротность Q = 2. Определите собственную частоту ω₀ колебаний этой системы.

75. Колебательный контур состоит из катушки индуктивностью L = 10 мГн, конденсатора емкостью C = 0,1 мкФ и резистора сопротивлением R = 20 Ом. Определите, через сколько полных колебаний амплитуда тока в контуре уменьшится в е раз.

76. Колебательный контур содержит катушку индуктивностью L = 25 мГн, конденсатор емкостью C = 10 мкФ и резистор сопротивлением R = 1 Ом. Конденсатор заряжен количеством электричества Q_m = 1 мКл. Определите: 1) период колебаний контура; 2) логарифмический декремент затухания колебаний; 3) уравнение зависимости изменения напряжения на обкладках конденсатора от времени.

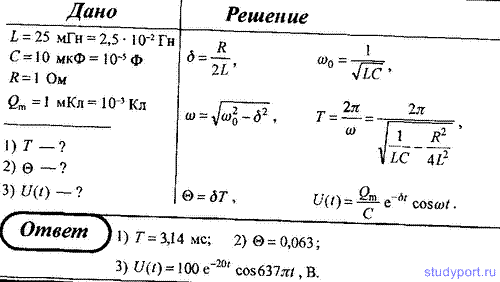
77. Определите логарифмический декремент затухания при котором энергия колебательного контура за N = 5 полных колебаний уменьшается в n = 8 раз.

78. Колебательный контур содержит катушку индуктивностью L = 6 мкГн, конденсатор емкостью C = 10 нФ и резистор сопротивлением R=10 Ом. Определите для случая максимума тока отношение энергии магнитного поля катушки к энергии электрического поля.

79. Определите добротность Q колебательного контура, состоящего из катушки индуктивностью L = 2 мГн, конденсатора емкостью C = 0,2 мкФ и резистора сопротивлением R = 1 Ом.

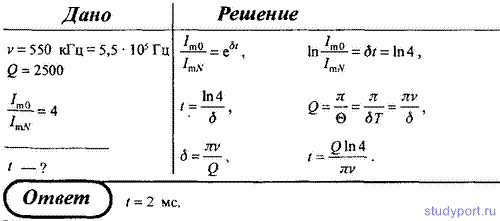
80. Частота v затухающих колебаний в колебательном контуре с добротностью Q = 2500 равна 550 кГц. Определите время, за которое амплитуда силы тока в этом контуре уменьшится в 4 раза.

81. Определите закон убывания заряда конденсатора со временем при его разряде в апериодическом режиме, т.е. когда δ = ω₀.

82. Определите минимальное активное сопротивление при разрядке лейденской банки, при котором разряд будет апериодическим. Емкость С лейденской банки равна 1,2 нФ, а индуктивность проводов составляет 3 мкГн.

84. Определите резонансную частоту колебательной системы, если собственная частота колебаний ν₀ = 300 Гц, а логарифмический декремент Θ = 0,2 .

85. Собственная частота ν₀ колебаний некоторой системы составляет 500 Гц. Определите частоту ν затухающих колебаний этой системы, если резонансная частота ν_рез = 499 Гц.

86. Период затухающих колебаний системы составляет 0,2 с, а отношение амплитуд первого и шестого колебаний равно 13. Определите резонансную частоту данной колебательной системы.

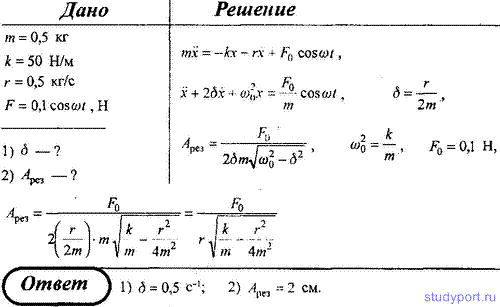
87. Гиря массой m = 0,5 кг, подвешенная на спиральной пружине жесткостью k = 50 Н/м, совершает колебания в вязкой среде с коэффициентом сопротивления r = 0,5 кг/с. На верхний конец пружины действует вынуждающая сила, изменяющаяся по закону F = 0,1 cos ωt, Н. Определите для данной колебательной системы: 1) коэффициент затухания δ; 2) резонансную амплитуду A_рез.

88. Гиря массой m = 400 г, подвешенная на спиральной пружине жесткостью k = 40 Н/м, опущена в масло. Коэффициент сопротивления r для этой системы составляет 0,5 кг/с. На верхний конец пружины действует вынуждающая сила, изменяющаяся по закону F = cos ωt, Н. Определите: 1) амплитуду вынужденных колебаний, если частота вынуждающей силы вдвое меньше собственной частоты колебаний; 2) частоту вынуждающей силы, при которой амплитуда вынужденных колебаний максимальна; 3) резонансную амплитуду.

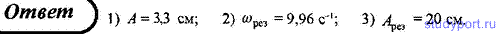
89. Гиря массой m = 200 г, подвешенная на спиральной пружине жесткостью k = 50 Н/м, совершает колебания в вязкой среде с коэффициентом сопротивления r = 0,2 кг/с. На верхний конец пружины действует вынуждающая сила, изменяющаяся по закону F = 0,2 cos ωt, Н. Определите: 1) частоту ν₀ собственных колебаний; 2) резонансную частоту ν_рез; 3) резонансную амплитуду A_рез; 4) статическое отклонение.

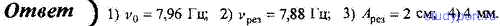
 90. Амплитуды двух вынужденных колебаний системы с одинаковыми собственными частотами при всех значениях частоты вынуждающей силы различаются вдвое. Определите, какой одной (и только одной) из величин (массой, коэффициентом сопротивления среды, коэффициентом упругости, амплитудой вынуждающей силы) отличаются эти системы.

91. В цепь колебательного контура, содержащего последовательно соединенные резистор сопротивлением R = 40 Ом, катушку индуктивностью L = 0,36 Гн и конденсатор емкостью C = 28 мкФ, подключено внешнее переменное напряжение с амплитудным значением U_m = 180 В и частотой ω = 314 рад/с. Определите: 1) амплитудное значение силы тока I_m в цепи; 2) сдвиг φ по фазе между током и внешним напряжением.

92. В цепь колебательного контура, содержащего катушку индуктивностью L = 0,2 Гн и активным сопротивлением R = 9,7 Ом, а также конденсатор емкостью C = 40 мкФ, подключено внешнее переменное напряжение с амплитудным значением U_m = 180 В и частотой ω = 314 рад/с. Определите: 1) амплитудное значение силы тока I_m в цепи; 2) разность фаз φ между током и внешним напряжением; 3) амплитудное значение напряжения U_Lm на катушке; 4) амплитудное значение U_Cm на конденсаторе.

93. Последовательно соединенные резистор с сопротивлением R = 110 Ом и конденсатор подключены к внешнему переменному напряжению с амплитудным значением U_m = 110 В. Оказалось, что амплитудное значение установившегося тока в цепи I_m = 0,5 А. Определите разность фаз между током и внешним напряжением.

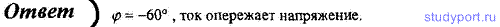
94. В колебательный контур, содержащий последовательно соединенные конденсатор и катушку с активным сопротивлением, подключено внешнее переменное напряжение, частоту которого можно менять, не меняя его амплитуды. При частотах внешнего напряжения ω₁ = 400 рад/с и ω₂ = 600 рад/с амплитуды силы тока в цепи оказались одинаковыми. Определите резонансную частоту тока.

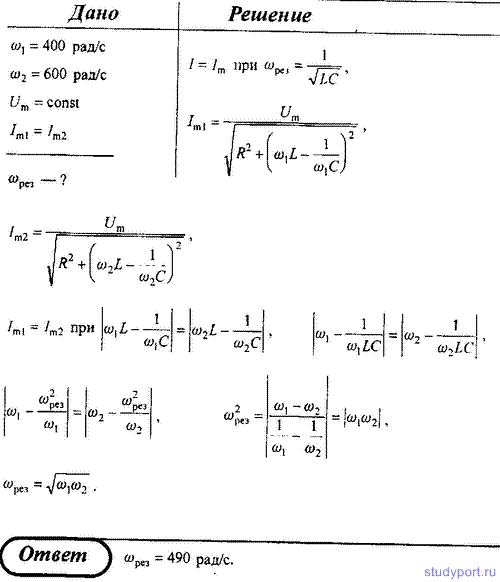
95. Колебательный контур содержит катушку индуктивностью L = 0,1 мГн, резистор сопротивлением R = 3 Ом, а также конденсатор емкостью C = 10 нФ. Определите среднюю мощность, потребляемую контуром, необходимую для поддержания в нем незатухающих колебаний с амплитудным значением напряжения на конденсаторе U_m = 2 В.

96. В цепь переменного тока напряжением 220 В и частотой 50 Гц последовательно включены резистор сопротивлением R = 100 Ом, катушка индуктивностью L = 0,5 Гн и конденсатор емкостью C = 10 мкФ. Определите амплитудное значение: 1) силы тока в цепи; 2) падения напряжения на активном сопротивлении; 3) падения напряжения на конденсаторе; 4) падения напряжения на катушке.

97. В цепь переменного тока частотой ν = 50 Гц включена катушка длиной l = 20 см и диаметром d = 5 см, содержащая N = 500 витков медного провода площадью поперечного сечения S = 0,6 мм². Определите, какая доля полного сопротивления катушки приходится на реактивное сопротивление. Удельное сопротивление меди ρ = 17 нОм*м.

98. В цепь переменного тока частотой ν = 50 Гц включена катушка длиной l = 30 см и площадью поперечного сечения S = 10 см², содержащая N = 1000 витков. Определите активное сопротивление катушки, если известно, что сдвиг фаз φ между напряжением и током составляет 30°.

99. К зажимам генератора присоединен конденсатор емкостью C = 0,15 мкФ. Определите амплитудное значение напряжения на зажимах, если амплитудное значение силы тока равно 3,3 А, а частота тока составляет 5 кГц.

100. Определите в случае переменного тока (ν = 50 Гц) полное сопротивление участка цепи, состоящего из параллельно включенного конденсатора емкостью C = 10 мкФ и резистора сопротивлением R = 50 Ом.

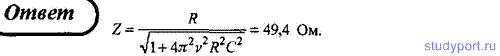
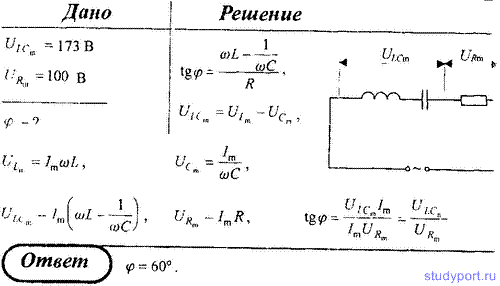
101. Цепь переменного тока состоит из последовательно соединенных катушки, конденсатора и резистора. Амплитудное значение суммарного напряжения на катушке и конденсаторе U_LCm = 173 В, а амплитудное значение напряжения на резисторе U_Rm = 100 В. Определите сдвиг фаз между током и внешним напряжением.

102. В цепь переменного тока частотой ν = 50 Гц последовательно включены резистор сопротивлением R = 100 Ом и конденсатор емкостью C = 22 мкФ. Определите, какая доля напряжения, приложенного к этой цепи, приходится на падение напряжения на конденсаторе.

103. В цепь переменного тока с частотой ν = 50 Гц и действующим значением напряжения U = 300 В последовательно включены конденсатор, резистор сопротивлением R = 50 Ом и катушка индуктивностью L = 0,1 Гн. Падения напряжения U₁ : U₂ = 1:2. Определите: 1) емкость конденсатора; 2) действующее значение силы тока.

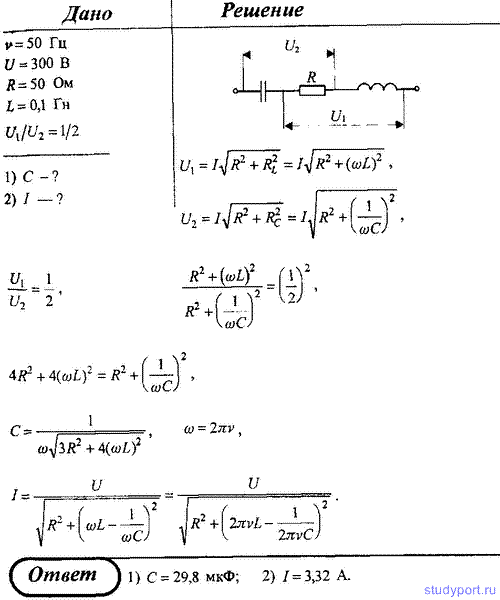
104. Генератор, частота которого составляет 32 кГц и амплитудное значение напряжения 120 В, включен в резонирующую цепь, емкость которой C = 1 нФ. Определите амплитудное значение напряжения на конденсаторе, если активное сопротивление цепи R = 5 Ом.

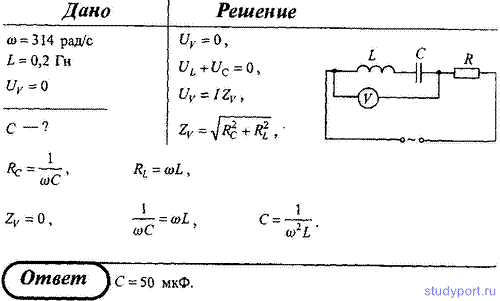
105. В цепи переменного тока с частотой ω = 314 рад/с вольтметр показывает нуль при L = 0,2 Гн. Определите емкость конденсатора.

106. В цепи переменного тока (см. рисунок  задачи 105) с частотой ν = 50 Гц вольтметр показывает нуль при значении C = 20 мкФ. Определите индуктивность катушки.

107. В приведенной на рисунке цепи переменного тока с частотой ν = 50 Гц сила тока внешней (неразветвленной) цепи равна нулю. Определите емкость С конденсатора, если индуктивность L катушки равна 1 Гн.

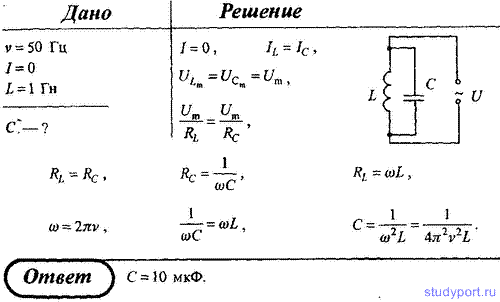
108. Активное сопротивление колебательного контура R = 0,4 Ом. Определите среднюю мощность <P>, потребляемую колебательным контуром, при поддержании в нем незатухающих гармонических колебаний с амплитудным значением силы тока I_m = 30 мА.

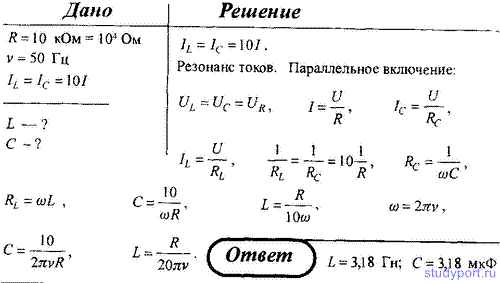
109. Как и какими индуктивностью L и емкостью С надо подключить катушку и конденсатор к резистору сопротивлением R = 10 кОм, чтобы ток через катушку и конденсатор был в 10 раз больше общего тока? Частота переменного напряжения ν = 50 Гц.

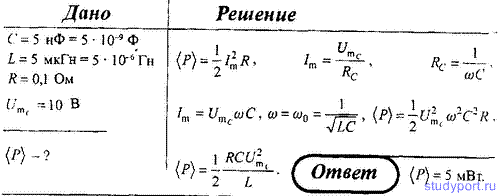
110. Колебательный контур содержит конденсатор емкостью C = 5 нФ и катушку индуктивностью L = 5 мкГн и активным сопротивлением R = 0,1 Ом. Определите среднюю мощность <P>, потребляемую колебательным контуром, при поддержании в нем незатухающих гармонических колебаний с амплитудным значением напряжения на конденсаторе U_mc = 10 В.

111. Колебательный контур содержит катушку индуктивностью L = 6 мкГн и конденсатор емкостью С = 1,2 нФ. Для поддержания в колебательном контуре незатухающих гармонических колебаний с амплитудным значением напряжения на конденсаторе U_mc = 2 В необходимо подводить среднюю мощность <P> = 0,2 мВт. Считая затухание в контуре достаточно малым, определите добротность данного контура.

112. В сеть переменного тока с действующим значением напряжения 120 В последовательно включены проводник с активным сопротивлением 10 Ом и катушка индуктивностью 0,1 Гн. Определите частоту ν тока, если амплитудное значение силы тока в цепи равно 5 А.

113. Диэлектрик, диэлектрическая проницаемость которого равна 2,8, используется в конденсаторе в качестве изолятора. Конденсатор, находясь под напряжением, поглощает некоторую мощность, причем при ν = 50 Гц коэффициент мощности cos φ = 0,1. Определите удельное сопротивление диэлектрика.

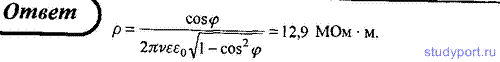
114. В цепь переменного тока напряжением U_m = 220 В и частотой 50 Гц включена катушка с активным сопротивлением. Сдвиг фаз между напряжением и током составляет π/6. Определите индуктивность катушки, если известно, что она поглощает мощность 445 Вт.

115. Цепь, состоящая из последовательно соединенных безындукционного резистора сопротивлением R = 100 Ом и катушки с активным сопротивлением, включена в сеть с действующим напряжением U = 300 В. Воспользовавшись векторной диаграммой, определите тепловую мощность, выделяемую на катушке, если действующее значение напряжения на сопротивлении и катушке соответственно равно U_R = 150 В и U_L = 250 В.