81. Тело массой m = 5 кг поднимают с ускорением a = 2 м/с2. Определить работу силы в течение первых пяти секунд.

82. Автомашина массой m = 1,8 т движется в гору, уклон которой
составляет 3 м на каждые 100 м пути. Определить: 1) работу, совершаемую
двигателем автомашины на пути 5 км, если коэффициент трения равен 0,1;
2) развиваемую двигателем мощность, если известно, что этот путь был
преодолен за 5 мин.

83. Определите работу, совершаемую при подъеме груза массой m = 50 кг по наклонной плоскости с углом наклона α = 30° к горизонту на расстояние s = 4 м, если время подъема t = 2 с, а коэффициент трения f = 0,06.
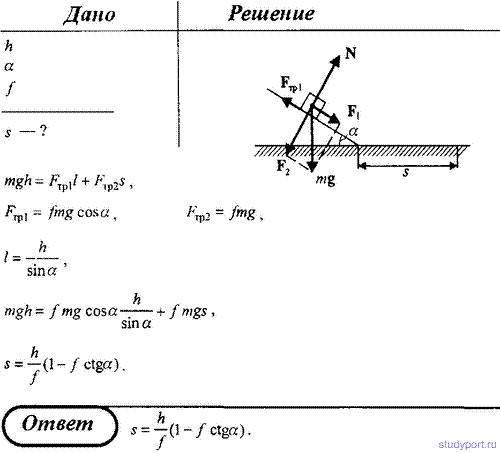
84. Тело скользит с наклонной плоскости высотой h и углом наклона α к
горизонту и движется далее по горизонтальному участку. Принимая
коэффициент трения на всем пути постоянным и равным f, определить
расстояние s, пройденное толом на горизонтальном участке, до полной
остановки.
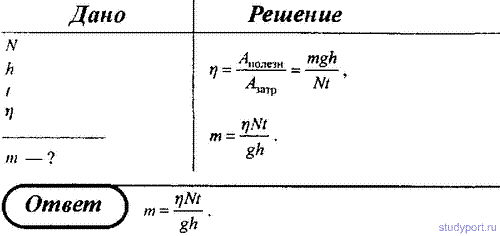
85. Насос мощностью N используют для откачки нефти с глубины h.
Определить массу жидкости, поднятой за время t, если КПД насоса равен η.
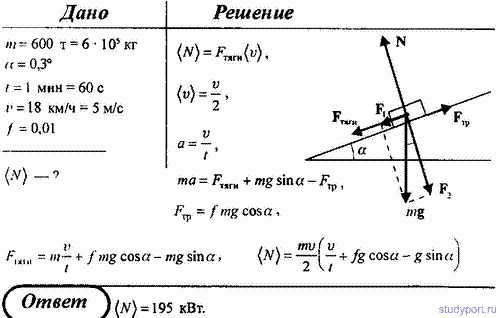
86. Поезд массой m = 600 т движется под гору с уклоном α = 0,3° и за
время t = 1 мин развивает скорость v = 18 км/ч. Коэффициент трения f =
0,01. Определить среднюю мощность локомотива.
87. Автомобиль массой т = 1,8 т спускается при выключенном двигателе с постоянной скоростью v = 54
км/ч по уклону дороги (угол к горизонту α = 3°). Определите, какой
должна быть мощность двигателя автомобиля, чтобы он смог подниматься на
такой же подъем с той же скоростью.

88. Материальная точка массой m = 1 кг двигалась под действием некоторой силы согласно уравнению s = A – B*t + C*t2 – D*t3 (B = 3 м/с, C = 5 м/с2, D = 1 м/с3). Определить мощность N, затрачиваемую на движение точки за время, равное 1 с.

89. Ветер действует на парус площадью S с силой F = A*S*ρ*(v0 – v)2/2, где А – некоторая постоянная; ρ – плотность воздуха; v0 – скорость ветра; v – скорость лодки. Определить скорость лодки при максимальной мгновенной мощности ветра.

90. Тело массой m поднимается без начальной скорости с поверхности
Земли под действием силы F, изменяющейся с высотой подъема y по закону F
= -2mg(l - Ay) (где А — некоторая положительная
постоянная), и силы тяжести mg , Определите: 1) весь путь подъема; 2)
работу силы F на первой трети пути подъема. Поле силы тяжести считать
однородным.
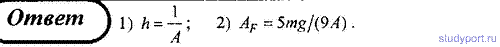
91. Тело массой m начинает двигаться под действием силы F = 2*t*i + 3*t2*j,
где i и j – соответственно единичные векторы координатных осей x и y.
Определить мощность N(t), развиваемую силой в момент времени t.

92. Тело массой m = 5 кг падает с высоты h = 20 м. Определить сумму
потенциальной и кинетической энергий тела в точке, находящейся от
поверхности Земли на высоте h1 = 5 м. Трением тела о воздух пренебречь. Сравнить энергию с первоначальной энергией тела.

93. Тело, падая с некоторой высоты, в момент соприкосновения с Землей обладает импульсом p = 100 кг * м/с и кинетической энергией T = 5 00 Дж Определите: 1) с какой начальной высоты тело падало, 2) массу тела.
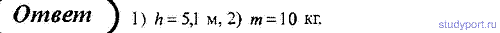
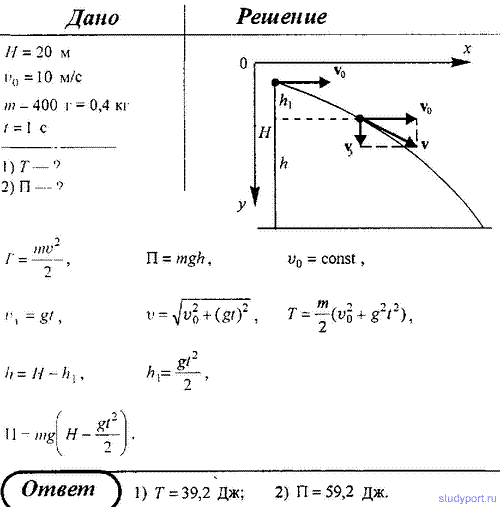
94. С башни высотой H = 20 м горизонтально со скоростью v0
= 10 м/с, брошен камень массой m = 400 г. Пренебрегая сопротивлением
воздуха, определить для момента времени t = 1 с после начала движения:
1) кинетическую энергию; 2) потенциальную энергию.
95. Автомашина массой m = 2000 кг останавливается за t = 6 c, пройдя
расстояние s = 30 м. Определить: 1) начальную скорость автомобиля; 2)
силу торможения.

96. Материальная точка массой m = 20 г движется по окружности
радиусом R = 10 см с постоянным тангенциальным ускорением. К концу
пятого оборота после начала движения кинетическая энергия материальной
точки оказалась равной 6,3 мДж. Определить тангенциальное ускорение.

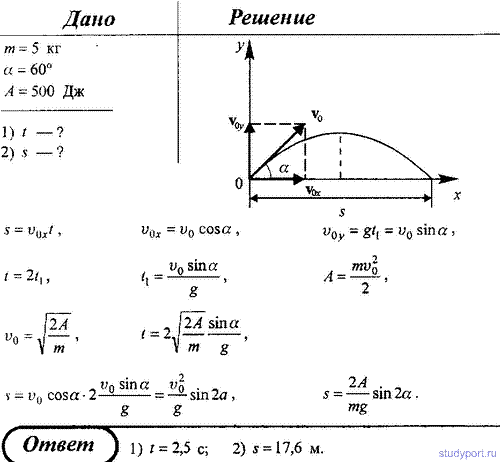
97. Ядро массой m = 5 кг бросают под углом α = 60° к горизонту,
совершая при этом работу 500 Дж. Пренебрегая сопротивлением воздуха,
определить: 1) через какое время ядро упадет на землю; 2) какое
расстояние по горизонтали оно пролетит.
98. Тело массой m = 0,5 кг бросают со скоростью v0 = 10 м/с под углом α = 30° к горизонту. Пренебрегая сопротивлением воздуха, определите кинетическую Т, потенциальную П и полную Е энергии тела: 1) через t = 0,4 с после начала движения; 2) в высшей точке траектории.
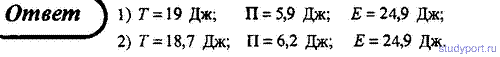
99. Тележка проходит расстояние s = 300 м под гору с уклоном α = 5° и
продолжает двигаться в гору с тем же уклоном. Принимая коэффициент
трения f постоянным и равным 0,05, определите расстояние x, на которое
поднимается тележка.

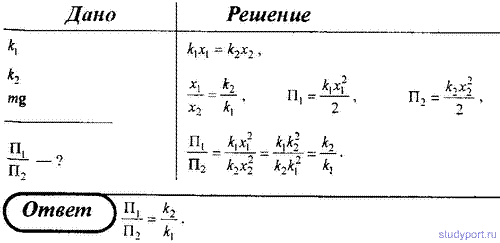
100. К нижнему концу пружины жесткостью k1 присоединена другая пружина жесткостью k2, к концу которой прикреплена гиря. Пренебрегая массой пружины, определить отношение потенциальных энергий пружин.
101. Тело массой m = 0,4 кг скользит с наклонной плоскости высотой h = 10
см и длиной l = 1 м. Коэффициент трения тела на всем пути f = 0,04.
Определите: 1) кинетическую энергию тела у основания плоскости; 2) путь,
пройденный телом на горизонтальном участке до остановки.
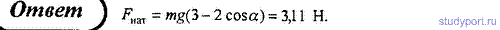
102. Тело брошено вертикально вверх со скоростью v0=20 м/с. Пренебрегая сопротивлением воздуха, определите, на какой высоте h кинетическая энергия тела будет равна его потенциальной энергии.

103. Тело массой m = 70 кг движется под действием постоянной силы F =
63 Н. Определить, на каком пути s скорость этого тела возрастает в n = 3
раза по сравнению с моментом времени, когда скорость тела была равна v0 = 1,5 м/с.
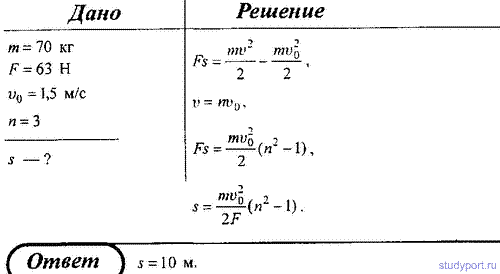
104. Подвешенный на нити шарик массой m = 200 г отклоняют на угол α =
45°. Определите силу натяжения нити в момент прохождения шариком
положения равновесия.
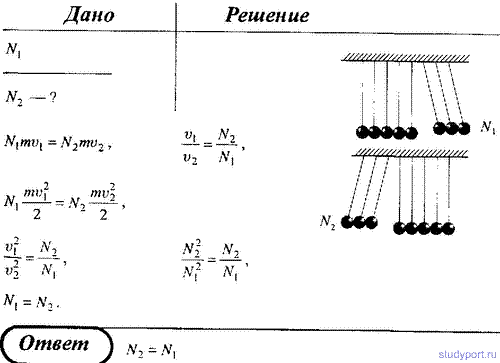
105. При абсолютно упругом ударе шаров одинаковой массой всегда
отскакивает столько шаров, сколько налетает. Докажите этот результат.
106. Тело брошено под углом α = 45° к горизонту со скоростью v0 = 15 м/с Используя закон сохранения энергии, определите скорость v тела в высшей точке его траектории.
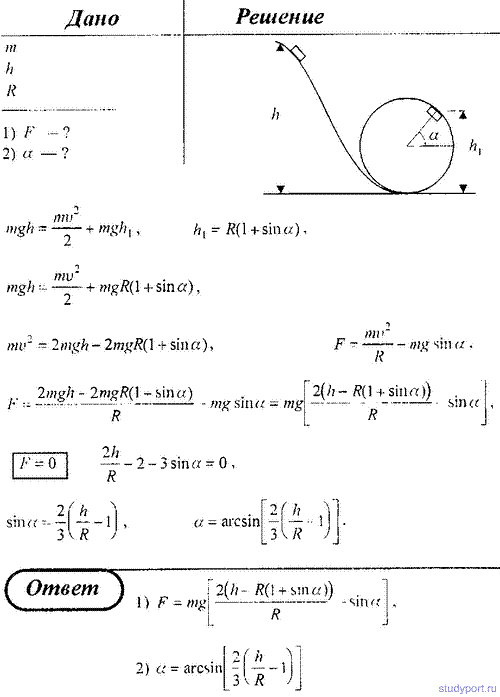
107. Шайба массой m скользит без трения с высоты h по желобу,
переходящему в петлю радиусом R. Определить: 1) силу давления F шайбы на
опору в точке, определяемой углом α (см. рис.); 2) угол α, при котором
произойдет отрыв шайбы.
108. Пренебрегая трением, определить наименьшую высоту h, с которой
должна скатываться тележка с человеком по желобу, переходящему в петлю
радиусом R = 6 м, и не оторваться от него в верхней точке петли.

109. Спортсмен с высоты h = 12 м падает на упругую сетку. Пренебрегая
массой сетки, определить, во сколько раз наибольшая сила давления
спортсмена на сетку больше его силы тяжести, если прогиб сетки под
действием только силы тяжести спортсмена x0 = 15 см.

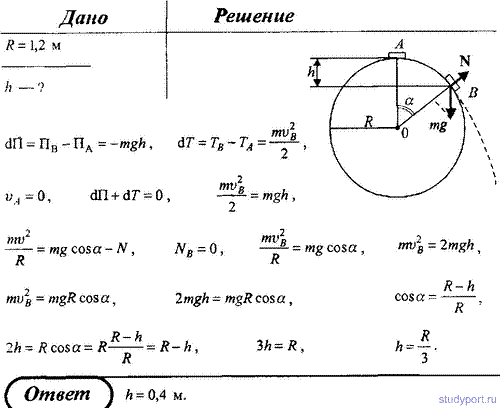
110. С вершины идеально гладкой сферы радиусом R = 1,2 м
соскальзывает небольшое тело. Определите высоту h (от вершины сферы), с
которой тело со сферы сорвется.
111. Два цилиндра массами m1 = 150 г и m2 = 300
г, соединенные сжатой пружиной, разошлись при внезапном освобождении
пружины в разные стороны. Пренебрегая силами сопротивления и учитывая,
что кинетическая энергия Т упругой деформации пружины составляет 1,8 Дж, определите: 1) скорость v1 движения первого цилиндра; 2) скорость v2 движения второго цилиндра.
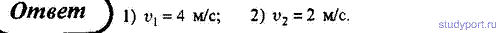
112. Гиря массой m = 10 кг падает с высоты h = 0,5 м на подставку,
скрепленную с пружиной жесткостью k = 30 Н/см. Определить при этом
смещение x пружины.

113. Пуля массой m = 15 г, летящая с горизонтальной скоростью v = 0,5
км/с, попадает в баллистический маятник М = 6 кг и застревает в нем.
Определить высоту h, на которую поднимается маятник, откачнувшись после
удара.

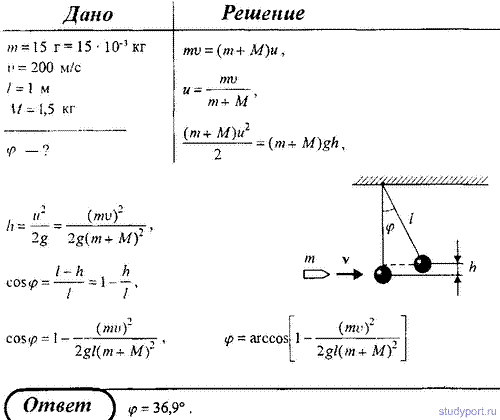
114. Пуля массой m = 15 г, летящая горизонтально, попадает в баллистический маятник длиной l = 1 ми массой М = 1,5 кг и застревает в нем. Маятник в результате этого отклонился на угол φ = 30°. Определите скорость пули.

115. Пуля массой m = 15 г, летящая горизонтально со скоростью v = 200
м/с, попадает в баллистический маятник длиной l = 1 м и массой М = 1,5
кг и застревает в нем. Определите угол отклонения φ маятника.
116. Пуля массой m = 12 г, летящая с горизонтальной скоростью v = 0,6 км/с, попадает в мешок с песком массой М = 10
кг, висящий на длинной нити, и застревает в нем. Определите: 1) высоту,
на которую поднимется мешок, отклонившись после удара; 2) долю
кинетической энергии, израсходованной на пробивание песка.
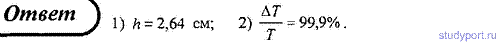
117. Зависимость потенциальной энергии П тела в центральном силовом
поле от расстояния r до центра поля задается функцией П(r) = А/r2 – B/r (A = 6 мкДж*м2,
B = 0,3 мДж*м). Определить, при каких значениях r максимальное значение
принимают: 1) потенциальная энергия тела; 2) сила, действующая на тело.

118. На рисунке представлена качественная зависимость потенциальной
энергии П взаимодействия двух частиц от расстояния r между ними.
Объясните, какому расстоянию между частицами соответствует равновесие,
при каком расстоянии оно является устойчивым и при каком — неустойчивым.
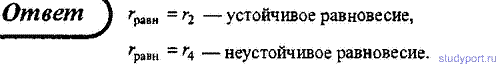
119. Сила, действующая на тело в некотором поле консервативных сил, описывается законом F = A(yi + xj), где А — некоторая постоянная; i и j — соответственно единичные векторы координатных осей x и у. Определите потенциальную энергию П(х, у) тела в этом поле.
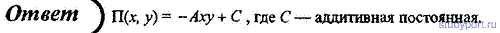
120. Металлический шарик падает вертикально на мраморный пол с высоты h1 = 80 см и отскакивает от него на высоту h2 = 72 см. Определить коэффициент восстановления материала шарика.

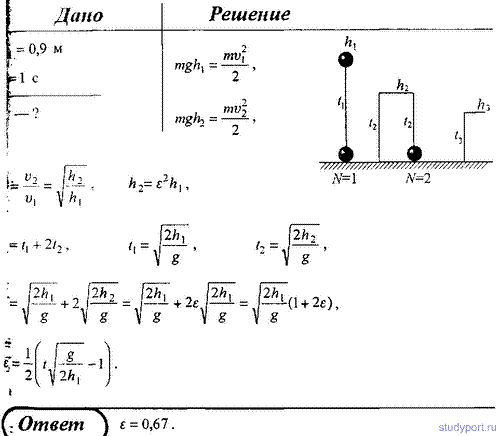
121. Шарик из некоторого материала, падая вертикально с высоты 0,9 м,
несколько раз отскакивает от пола. Определите коэффициент
восстановления материала шарика при ударе о пол, если с момента падения
до которого удара прошло время t = 1 c.
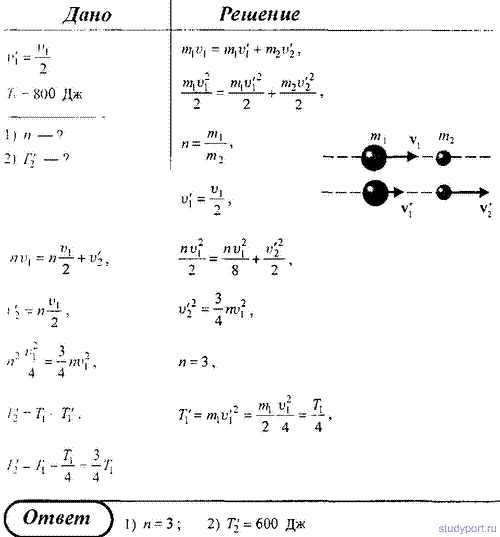
122. При центральном упругом ударе движущееся тело массой m1 ударяется в покоящееся тело массой m2,
в результате чего скорость первого тела уменьшается в 2 раза.
Определить: 1) во сколько раз масса первого тела больше массы второго
тела; 2) кинетическую энергию T2 второго тела непосредственно после удара, если первоначальная кинетическая энергия T1 первого тела равна 800 Дж.
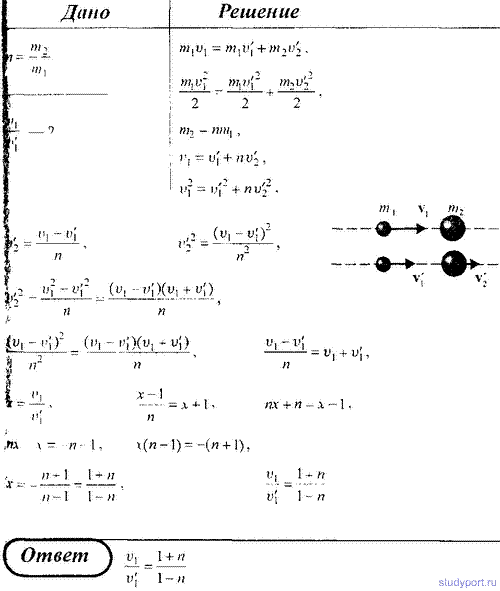
123. Определить, во сколько раз уменьшится скорость шара, движущегося со скоростью v1,
при его соударении с покоящимся шаром, масса которого в n раз больше
массы налетающего шара. Удар считать центральным абсолютно упругим.
124. Тело массой m1 =3 кг движется со скоростью v1
= 2 м/с и ударяется о неподвижное тело такой же массы. Считая удар
центральным и неупругим, определите количество теплоты, выделившееся при
ударе.

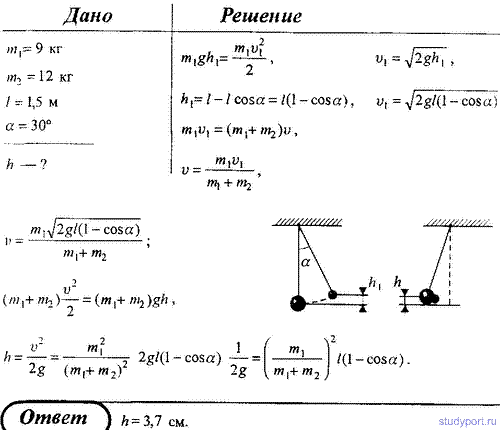
125. Два шара массами m1 = 9 кг и m2 = 12 кг
подвешены на нитях длиной l = 1,5 м. Первоначально шары соприкасаются
между собой, затем меньший шар отклонили на угол α = 30° и отпустили.
Считая удар неупругим, определите высоту h, на которую поднимутся оба
шара после удара.
126. Два шара массами m1 = 3 кг и m2 = 2 кг
подвешены на нитях длиной l = 1 м. Первоначально шары соприкасаются
между собой, затем больший шар отклонили от положения равновесия на угол
α = 60° и отпустили. Считая удар упругим, определите скорость второго
шара после удара.

127. Два шара массами m1 = 200 г и m2 = 400
г подвешены на нитях длинной l = 67,5 см. Первоначально шары
соприкасаются между собой, затем первый шар отклонили от положения
равновесия на угол α = 60° И отпустили. Считая удар упругим, определите, на какую высоту h поднимется второй шар после удара.
<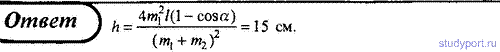 /p> /p>
128. Шар сталкивается с другим покоящимся шаром такой же массы.
Докажите, что в случае упругого, но не центрального удара угол между
направлениями скоростей после удара составляет π/2.

|