249. В лабораторной системе отсчета в точках с координатами x1 и x2 = x1 + l0 одновременно происходят события 1 и 2, причем l0
= 1,4 км. Определить: 1) расстояние l`, фиксируемое наблюдателем в
системе отсчета, связанной с ракетой, которая со скоростью v = 0,6с в
отрицательном направлении оси х; 2) время между этими событиями,
фиксируемое наблюдателем в системе отсчета, связанной с ракетой.

250. Две нестабильные частицы движутся в системе отсчета К в одном
направлении вдоль одной прямой с одинаковой скоростью v = 0,6с.
Расстояние между частицами в системе К равно 64 м. Обе частицы распались
одновременно в системе К`, которая связана с ними. Определить
промежуток времени между распадом частиц в системе К.
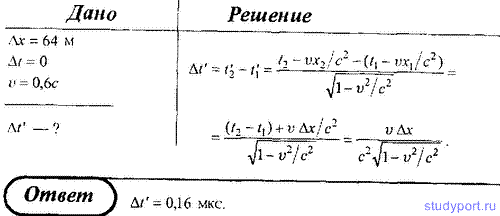
252. Определите, во сколько раз увеличивается время жизни
нестабильной частицы (по часам неподвижного наблюдателя), если она
начинает двигаться со скоростью 0,9с.
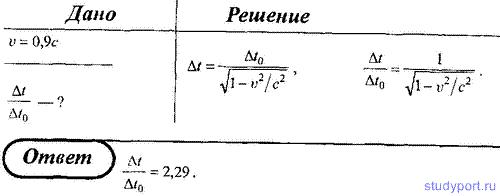
253. Собственное время жизни частицы отличается на 1% от времени жизни по неподвижным часам. Определить β = v/c.

254. Космический корабль движется со скоростью v = 0,8с по направлению к Земле Определите расстояние, пройденное им в системе отсчета, связанной с Землей (системе К), за t0 = 0,5с, отсчитанное по часам в космическом корабле (системе К').

255. Мюоны, рождаясь в верхних слоях атмосферы, при скорости v =
0,995c пролетают до распада l = 6 км. Определить: 1) собственную длину
пути, пройденную ими до распада; 2) время жизни мюона для наблюдателя на
Земле; 3) собственное время жизни мюона.

257. Определите относительную скорость движения, при которой реля сокращение линейных размеров тела составляет 10%.
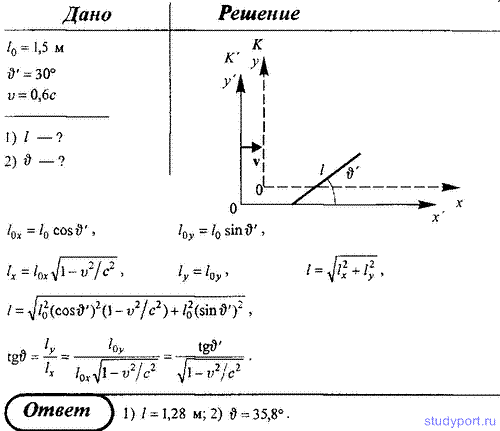
258. В системе К` покоится стержень (собственная длина l0 =
1,5 м), ориентированный под углом ψ` = 30 градусов к оси Ох`. Система
К` движется относительно системы К со скоростью v = 0,6с. Определить в
системе К: 1) длину стержня l; 2) соответствующий угол ψ.
259. Определите собственную длину стержня, если в лабораторной системе его скорость v = 0,6с , длина l = 1,5 м и угол между ним и направлением движения ψ = 30° .

260. Пользуясь преобразованиями Лоренца, выведите релятивистский
закон сложения скоростей, если переход происходит от системы К к системе
К`. 2

261. Космический корабль удаляется от Земли с относительной скоростью v1 = 0,8с , а затем с него стартует ракета (в направлении от Земли) со скоростью v2 = 0,8с относительно корабля. Определите скорость u ракеты относительно Земли.

262. Ионизированный атом, вылетев из ускорителя со скоростью 0,8с,
испустил фотон в направлении своего движения. Определить скорость фотона
относительно ускорителя.

263. Две ракеты движутся навстречу друг другу относительно
неподвижного наблюдателя с одинаковой скоростью, равной 0,5с. Определить
скорость сближения ракет, исходя из закона сложения скоростей: 1) в
классической механике; 2) в специальной теории относительности.

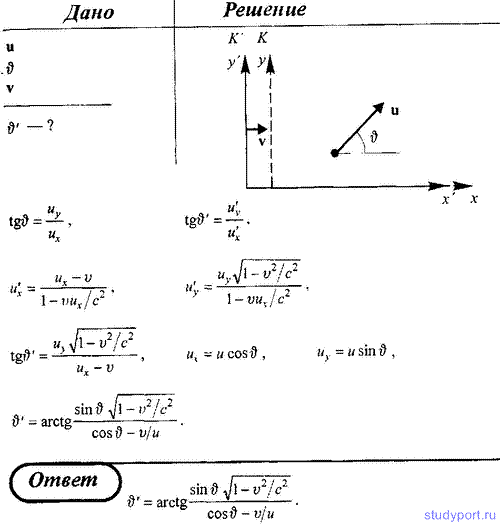
264. Релятивистская частица движется в системе К со скоростью u под
углом ψ к оси х. Определить соответствующий угол в системе К`,
движущейся со скоростью v относительно системы К в положительном
направлении оси х, если оси х и х` обеих систем совпадают.
266. Воспользовавшись тем, что интервал является инвариантной
величиной по отношению к преобразованиям координат, определить
расстояние, которое пролетел π-мезон с момента рождения до распада, если
время его жизни в этой системе отсчета Δt = 4,4 мкс, а собственное
время жизни Δt0 = 2,2 мкс.
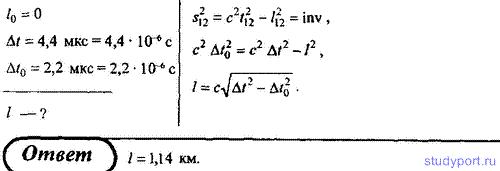
267. Частица движется со скоростью v = 0,8с. Определите отношение полной энергии релятивистской частицы к ее энергии покоя.

268. Определите, на сколько процентов полная энергия релятивистс элементарной частицы, вылетающей из ускорителя со скоро v = 0,75с, больше ее энергии покоя.

269. Определите скорость движения релятивистской частицы, если ее полная энергия в два раза больше энергии покоя.

270. Определите релятивистский импульс протона, если скорость его движения v = 0,8с.
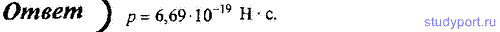
271. Определите скорость, при которой релятивистский импульс час превышает ее ньютоновский импульс в 3 раза.
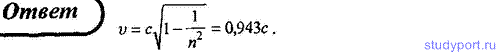
272. Определить зависимость скорости частицы (масса частицы m) от
времени, если движение одномерное, сила постоянна и уравнение движения
релятивистское.

273. Полная энергия релятивистской частицы в 8 раз превышает ее энергию покоя. Определите скорость этой частицы.

274. Кинетическая энергия частицы оказалась равной её энергии покоя. Определить скорость частицы.

275. Определить релятивистский импульс p и кинетическую энергию l протона, движущегося со скоростью v = 0,75с.
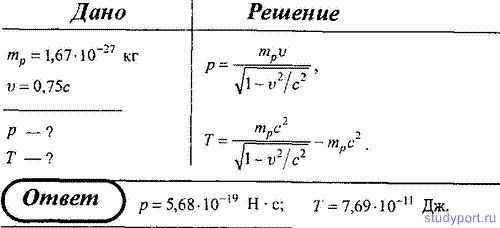
276. Определить кинетическую энергию электрона, если полная энергия
движущегося электрона втрое больше его энергии покоя. Ответ выразить в
электрон-вольтах.
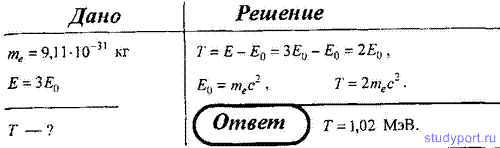
277. Определить, какую ускоряющую разность потенциалов должен пройти протон, чтобы его скорость составила 90% скорости света.
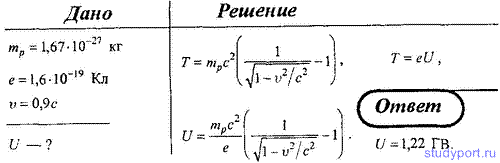
278. Определить, какую ускоряющую разность потенциалов должен пройти
электрон, чтобы его продольные размеры уменьшились в два раза.

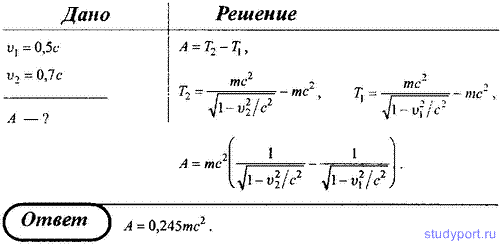
279. Определить работу, которую необходимо совершить, чтобы увеличить скорость частицы от 0,5с до 0,7с.
281. Определить релятивистский импульс электрона, кинетическая энергия которого T = 1 ГэВ.

282. Доказать, что выражение релятивистского импульса р = корень(T*(T+2mc2)/c при v << с переход в соответствующее выражение классической механики.
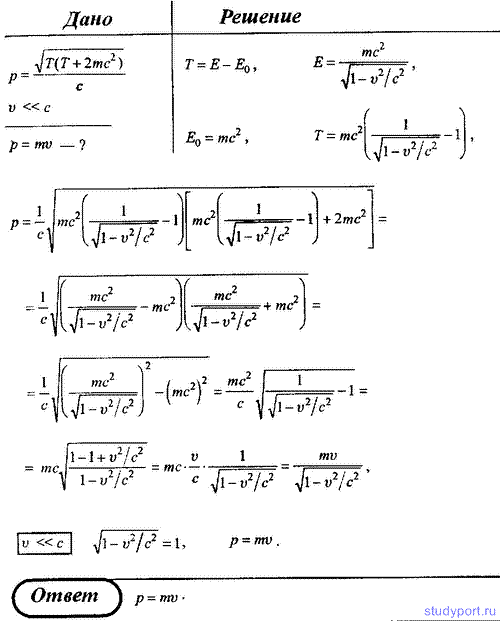
283. Докажите, что для релятивистской частицы величина E2 – p2*c2 является инвариантной, т.е. имеет одно и то же значение во всех инерциальных системах отсчета.

284. Определить энергию, которую необходимо затратить, чтобы
разделить ядро дейтрона на протон и нейтрон. Массу ядра дейтрона принять
равной 3,343*10-26 кг. Ответ выразите в электрон-вольтах.

285. Определите энергию связи ядра 147N. Примите массу ядра азота равной 2,325 * 10-26 кг. Ответ выразите в электрон-вольтах.

|