43. Тело массой m = 2 кг движется прямолинейно по закону s = A – B*t + C*t² – D*t³ (C = 2 м/c², D = 0,4 м/c³) Определить силу, действующую на тело в конце первой секунды движения.

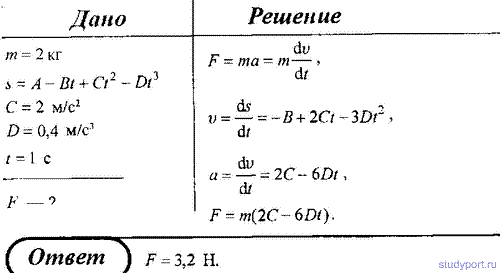
44. Тело массой m движется так, что зависимость пройденного пути от времени описывается уравнением s = A * cos(ωt), где А и ω — постоянные. Запишите закон изменения силы от времени.

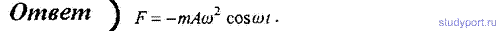
45. К нити подвешен груз массой m = 500 г. Определите силу натяжения нити, если нить с грузом: 1) поднимать с ускорением 2 м/с²; 2) опускать с ускорением 2 м/с².

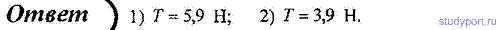
46. Два груза (m₁ = 500 г и m₂ = 700 г) связаны невесомой нитью и лежат на гладкой горизонтальной поверхности. К грузу m₁ приложена горизонтально направленная сила F = 6 Н. Пренебрегая трением, определите 1) ускорение грузов; 2) силу натяжения нити.

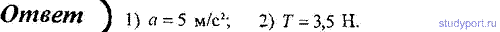
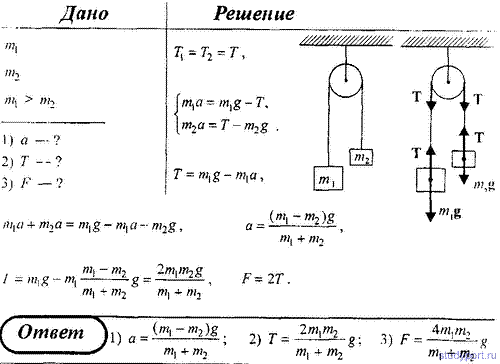
47. Простейшая машина Аттвуда, применяется для изучения закона равноускоренного движения, представляет собой два груза с не равными массами m₁ и m₂ (например m₁ > m₂), которые подвешены на легкой нити, перекинутой через неподвижный блок. Считая нить и блок невесомыми и пренебрегая трением в оси блока, определить: 1) ускорение грузов; 2) силу натяжения T; 3) силу F, действующую на ось блока.

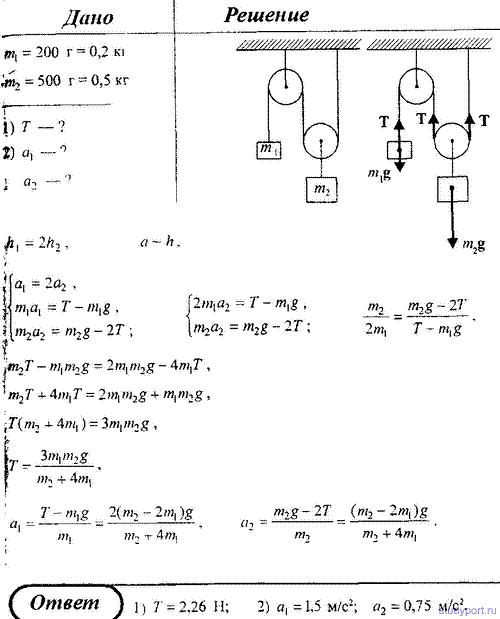
48. На рисунке изображена система блоков, к которым подвешены грузы массами m₁ = 200 г и m₂ = 500 г. Считая, что груз m₁ поднимается, а подвижный блок с m₂ опускается, нить и блок невесомы, силы трения отсутствуют, определить: 1) силу натяжения нити Т; 2) ускорение, с которыми движутся грузы.

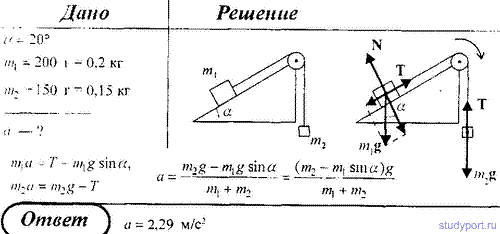
49. В установке на рисунке угол α наклонной плоскости с горизонтом равен 20°, массы тел m₁ = 200 г и m₂ = 150 г. Считая нить и блок невесомыми и пренебрегая силами трения, определить ускорение, с которыми будут двигаться тела, если тело m₂ опускается.

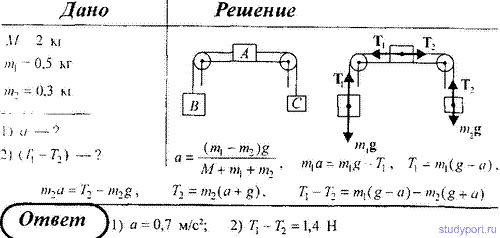
50. Тело А массой М = 2 кг находится на горизонтальном столе и соединено нитями посредством блоков с телами В (m₁ = 5 кг) и С (m₂ = 0,3 кг) Считая нити и блоки невесомыми и пренебрегая силами трения, определить: 1) ускорение, у которым будет двигаться эти тела; 2) разность сил натяжения нитей.

51. В установке углы α и β наклонных плоскостей с горизонтом соответственно равны 30 и 45°, массы тел m₁ = 0,45 кг и m₂ = 0,5 кг. Считая нить и блок невесомыми и пренебрегая силами трения, определите: 1) ускорение, с которым движутся тела; 2) силу натяжения нити.

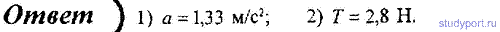
52. Тело массой m движется в плоскости xy по закону x = A*cos(ω*t), y = B*sin(ω*t), где A, B и ω – некоторые постоянные. Определить модуль силы, действующей на это тело.

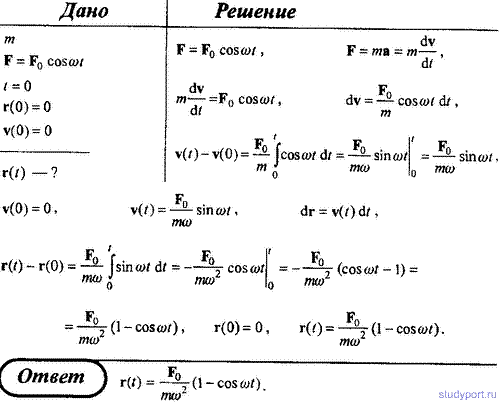
53. Частица массой m движется под действием силы F = F₀*cos(ω*t), где F₀ и ω – некоторые постоянные. Определите положение частицы, т.е. выразите её радиус-вектор r как функцию времени, если в начальный момент времени t = 0, r(0) = 0 и v(0) = 0.

54. На тело массой m =10 кг, лежащее на наклонной плоскости (угол α равен 20°), действует горизонтально направленная сила F = 8 Н. Пренебрегая трением, определите: 1) ускорение тела; 2) силу, с которой тело давит на плоскость.

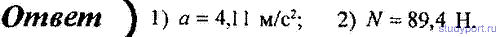
55. Тело массой m = 2 кг падает вертикально с ускорением a = 5 м/с². Определите силу сопротивления при движении этого тела.

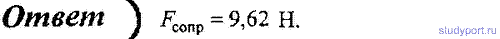
56. С вершины клина, длина которого l = 2 м и высота h = 1 м, начинает скользить небольшое тело Коэффициент трения между телом и клипом f = 0,15. Определите: 1) ускорение, с которым движется тело, 2) время провождения тела вдоль клина; 3) скорость тела у основания клина.

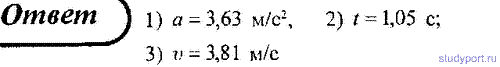
57. По наклонной плоскости с углом α наклона к горизонту, равным 30°, скользит тело. Определите скорость тела в конце второй секунды от начала скольжения, если коэффициент трения f = 0,15.

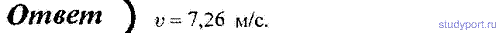
58. Вагон массой m = 1 т спускается по канатной железной дороге с уклоном α = 15° к горизонту. Принимая коэффициент трения f = 0,05, определите силу натяжения каната при торможении вагона в конце спуска, если скорость вагона перед торможением v₀ = 2,5 м/с, а время торможения t = 6 с.

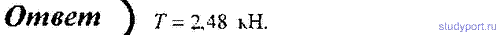
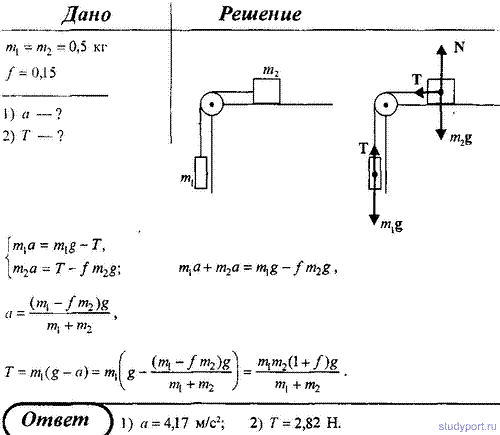
59. Грузы одинаковой массы (m₁ = m₂ = 0,5 кг) соединены нитью и перекинуты через невесомый блок, укрепленный на конце стола. Коэффициент трения груза m₂ о стол f = 0,15. Пренебрегая трением в блоке, определить: 1) ускорение, с которым движется грузы; 2) силу натяжения нити.

60. Система грузов массами m₁ = 0,5 кг и m₂ = 0,6 кг находятся в лифте, движущемся вверх с ускорением a = 4,9 м/с². Определить силу натяжения нити, если коэффициент трения между грузом массы m₁ и опорой f = 0,1.

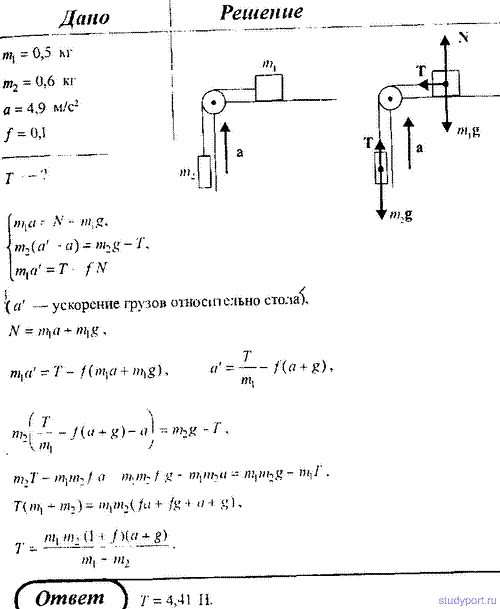
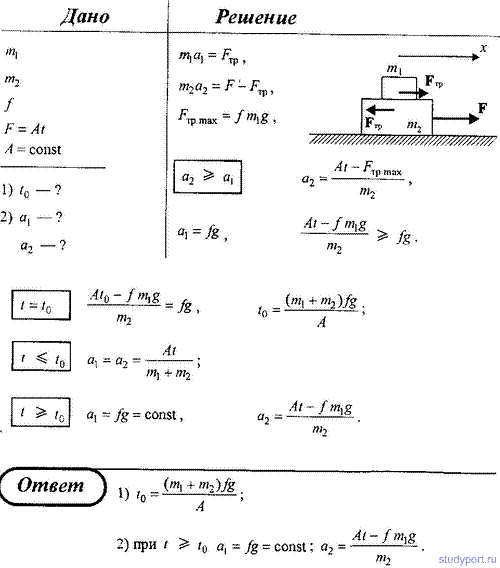
61. На гладкой горизонтальной поверхности находится доска массой m₂, на которой лежит брусок массой m₁. Коэффициент трения бруска о поверхность доски равен f. К доске приложена горизонтальная сила F, зависящая от времени по закону F = A*t, где A – некоторая постоянная. Определить: 1) момент времени t₀, когда доска начнет выскальзывать из-под бруска; 2) ускорение бруска а₁ и доски а₂ в процессе движения.

62. В установке угол α наклона плоскости с горизонтом равен 30°. Массы тел одинаковы (m = 1 кг). Считая нить и блок невесомыми и пренебрегая трением в оси блока, определите силу давления на ось, если коэффициент трения между наклонной плоскостью и лежащим на ней телом f = 0,1.

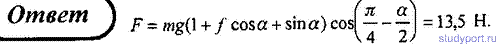
63. На наклонную плоскость с углом наклона к горизонту α = 35° положена доска массой m₂ = 2 кг, а на доску — брусок массой m₁ = 1 Kг. Коэффициент трения между бруском и доской f₁ = 0,1, а между доской и плоскостью f₂ = 0,2 . Определите: 1) ускорение бруска; 2) ускорение доски, 3) коэффициент трения f₂', при котором доска не будет двигаться.

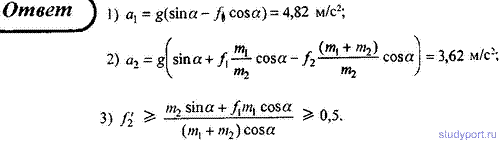
64. Снаряд массой m = 5 кг, вылетевший из орудия, верхней точке траектории имеет скорость v = 300 м/с. В этой точке он разорвался на два осколка, причем больший осколок массой m₁ полетел в обратном направлении со скоростью v₁ = 100 м/с. Определить скорость v₂ второго меньшего осколка.

65. Лодка массой M = 150 кг и длиной l = 2,8 м стоит неподвижно в стоячей воде. Рыбак массой m = 90 кг в лодке переходит с носа на корму. Пренебрегая сопротивлением воды, определите, на какое расстояние s при этом сдвинется лодка.

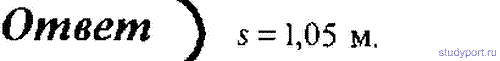
66. Снаряд, вылетевший из орудия со скоростью v₀ , разрывается на два одинаковых осколка в верхней точке траектории на расстоянии l (по горизонтали). Один из осколков полетел в обратном направлении со скоростью движения снаряда до разрыва. Пренебрегая сопротивлением воздуха, определите, на каком расстоянии (по горизонтали) от орудия упадет второй осколок.

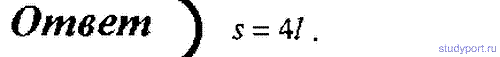
67. Платформа с песком общей массой M = 2 т стоит на рельсах на горизонтальном участке пути. В песок попадает снаряд массой m = 8 кг и застревает в нем. Пренебрегая трением, определите, с какой скоростью будет двигаться платформа, если в момент попадания скорость снаряда v = 450 м/с, а ее направление — сверху вниз под углом α = 30° к горизонту.

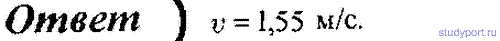
68. На железнодорожной платформе, движущейся по инерции со скоростью v₀ = 3 км/ч, укреплено орудие. Масса платформы с орудием M = 10 т. Ствол орудия направлен в сторону движения платформы. Снаряд массой m = 10 кг вылетает из ствола под углом α = 60° к горизонту. Определить скорость v снаряда (относительно Земли), если после вылета скорость платформы уменьшилась в n = 2 раза.

69. Две легкие тележки (массы соответственно m₁ и m₂ = 2m₁) соединены между собой сжатой, связанной нитью пружиной. Пережигая нить, пружина распрямляется, и тележка разъезжается в разные стороны. Считая коэффициент трения для обеих тележек одинаковый, определить: 1) v₁/v₂ – отношение скоростей движения тележек; 2) t₁/t₂ – отношение времени, в течении которого тележки движутся; 3) s₁/s₂ – отношение путей пройденных тележкой.

70. Две одинаковые тележки массой М каждая движутся по инерции (без трения) друг за другом с одинаковой скоростью v₀. В какой-то момент времени человек массой m, находящийся на задней тележке, прыгнул на переднюю тележку со скоростью u относительно своей тележки. Определите скорость v₁ передней тележки.

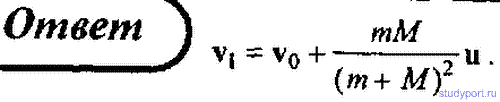
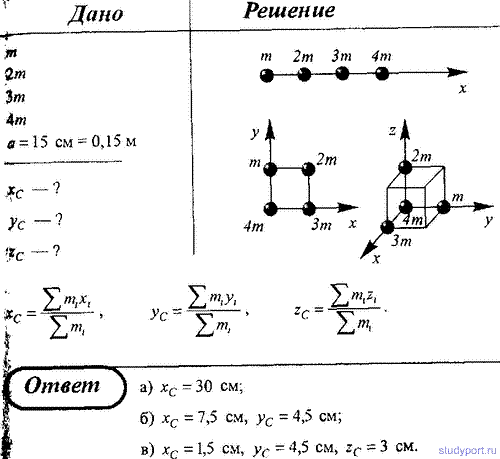
71. Определите положение центра масс системы, состоящей из четырех шаров, массы которых равны соответственно m, 2m, Зm  и 4m, в следующих случаях: а) шары расположены на одной прямой; б) шары расположены по вершинам квадрата; в) шары расположены по четырем смежным вершинам куба. Во всех случаях расстояние между соседними шарами равно 15 см. Направление координатных осей показано на рисунке.

72. Определите положение центра масс половины круглого диска радиусом R, считая его однородным.

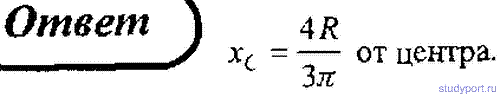
73. Определите координаты центра масс системы, состоящей из четырех шаров массами 2m, Зm, 4m и т, которые расположены в вершинах и в центре равностороннего треугольника со стороной a = 20 см. Направление координатных осей показано на рисунке.

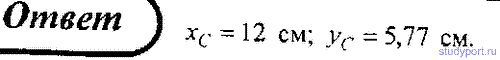
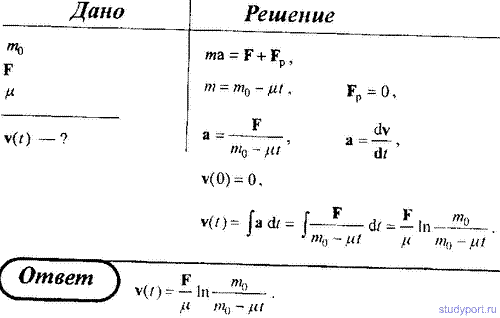
74. нагруженная песком железнодорожная платформа с начальной массой m₀ начинает движение из состояния покоя под действием постоянной силы тяги F. Через отверстие в дне платформы высыпается песок с постоянной скоростью μ (кг/с) Определить v(t), т.е. зависимость скорости платформы от времени.

75. На катере массой m = 4,5 т находится водомет, выбрасывающий со скоростью u = 6 м/с относительно катера назад μ = 25 кг/с воды. Пренебрегая сопротивлением движению катера, определите: 1) скорость катера через t = 3 мин после начала движения; 2) предельно возможную скорость катера.

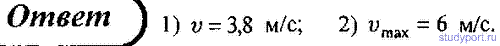
76. Ракета, масса которой в начальный момент времени М = 2 кг, запущена вертикально вверх. Относительная скорость выхода продуктов сгорания u = 150 м/с, расход горючего μ = 0,2 кг/с. Пренебрегая сопротивлением воздуха, определить ускорение a ракеты через t = 3 с после начала её движения. Поле силы тяжести считать однородным.

77. Ракета, масса М которой в начальный момент времени равна 300 г, начинает выбрасывать продукты сгорания с относительной скоростью u = 200 м/с. Расход горючего μ = 100 г/с. Пренебрегая сопротивлением воздуха и внешним силовым полем, определить: 1) за какой промежуток времени скорость ракеты станет равной v₁ = 50 м/с; 2) скорость v₂, которой достигнет ракета, если масса заряда m₀ = 0,2 кг.

78. Ракета с начальной массой m₀, начиная движение из состояния покоя, к некоторому моменту времени t израсходовав топливо массой m, развивает скорость v. Пренебрегая сопротивлением воздуха и внешним силовым полем, определите зависимость v от m, если скорость истечения топлива относительно ракеты равна u.

79. Ракета поднимается с нулевой начальной скоростью вертикально вверх. Начальная масса ракеты m₀, скорость истечения газа относительно ракеты постоянна и равна u. Пренебрегая сопротивлением воздуха, выразите скорость ракеты v в зависимости от m и t (m — масса ракеты; t — время ее подъема). Поле силы тяжести считайте однородным.

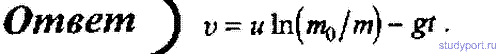
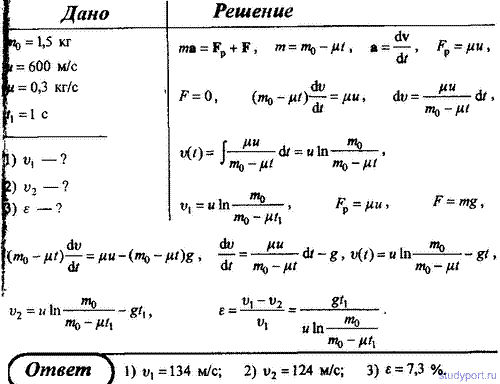
80. Ракета с начальной массой m₀ = 1,5 кг, начинает движение из состояния покоя вертикально вверх, выбрасывая непрерывную струю газов с постоянной скоростью относительно нее скорости u = 600 м/с. Расход газа μ = 0,3 кг/c. Определить, какую скорость приобретет ракета через 1 секунду после начала движения, если она движется: 1) при отсутствии внешних сил; 2) в однородном поле силы тяжести. Оценить относительную погрешность, сделанную для данных условий задачи при пренебрежении внешним силовым полем.