215. Докажите, что отношение числового значения орбитального магнитного момента p_m электрона к числовому значению его орби механического момента L_e (гиромагнитное отношение орбитальных моментов) одинаково для любой орбиты, по которой движется электрон.

216. Принимая, что электрон в невозбужденном атоме водорода движется по круговой орбите радиусом r = 52,8 пм, определить: 1) магнитный момент p_m эквивалентного кругового тока; 2) орбитальный механический момент L_e электрона; 3) исходя из полученных числовых значений, гиромагнитное отношение орбитальных моментов, доказав, то оно совпадает со значением, определяемым универсальными постоянными.

218. В однородное магнитное поле вносится длинный вольфрамовый стержень (магнитная проницаемость вольфрама μ = 1,0176). Определить, какая доля суммарного магнитного поля в этом стержне определяется молекулярными токами.

219. Напряженность однородного магнитного поля в пластине равна 5 А/м. Определить магнитную индукцию поля, создаваемого молекулярными токами, если магнитная восприимчивость платины равна 3,6*10⁴.

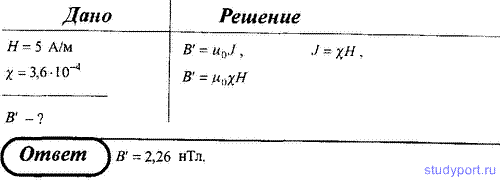
220. По круговому контуру радиусом r = 40 см, погруженному в жидкий кислород, течет ток I = 1 А. Определить намагниченность в центре этого контура. Магнитная восприимчивость жидкого кислорода χ = 3,4*10^-3.

221. По обмотке соленоида индуктивностью L = 3 мГн, находящегося в диамагнитной среде, течет ток I = 0,4 А. Соленоид имеет длину l = 45 см, площадь поперечного сечения S = 10 см² и число витков N = 1000. Определить внутри соленоида: 1) магнитную индукцию; 2) намагниченность.

222. Соленоид, находящийся в диамагнитной среде, имеет длину l = 30 см. площадь поперечного сечения S = 15 см² и число витков N = 500 . Индуктивность соленоида L = 1.5 мГн, а сила тока, протекающего по нему, I = 1 A. Определите: 1) магнитную индукцию внутри соленоида. 2) намагниченность внутри соленоида.

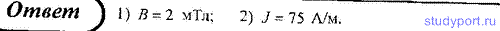
223. Индукция магнитного поля в железном стержне В = 1,2 Тл. Определить для него намагниченность, если зависимость В(Н) для данного сорта ферромагнетика представлена на рисунке.

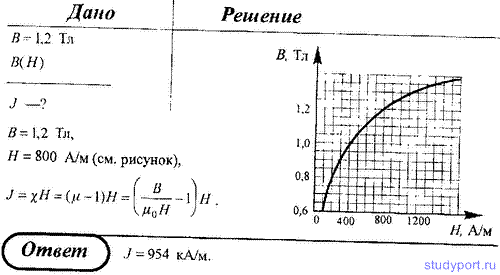
224. Железный сердечник длиной l = 0,5 м малого сечения (d << l) содержит 400 витков. Определите магнитную проницаемость железа при силе тока I = 1 А. Используйте график из задачи 223

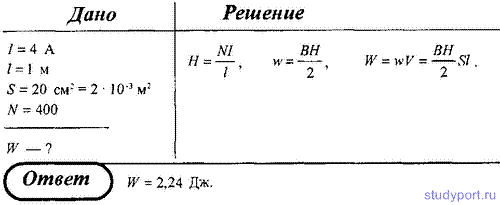
225. По обмотке соленоида, в который вставлен железный сердечник (график зависимости индукции магнитного поля от напряжения представлен в задаче 223), течет ток I = 4 А. Соленоид имеет длину l = 1 м, площадь поперечного сечения S = 20 см² и число витков N = 400. Определить энергию магнитного поля соленоида.

226. Обмотка тороида с железным сердечником имеет N = 151 виток. Средний радиус r тороида составляет 3 см. Сила тока I через обмотку равна 1 А. Определите для этих условий: 1) индукцию магнитного поля внутри тороида; 2) намагниченность сердечника; 3) магнитную проница сердечника. Используйте график зависимости B от H, приведенный в задаче 223.

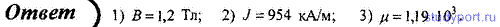
227. На железном сердечнике в виде тора со средним диаметром d = 10 мм намотана обмотка с общим числом витков N = 600. В сердечнике сделана узкая поперечная прорезь шириной b = 1,5 мм (рисунок к задаче 228). При силе тока через обмотку I = 4 А магнитная индукция в про B₀ = 1,5 Тл. Пренебрегая рассеянием поля на краях прорези, определите магнитную проницаемость железа для данных условий.

228. На железном сердечнике в виде тора со средним диаметром d = 70 мм намотана обмотка с общим числом витков N = 600. В сердечнике сделана узкая поперечная прорезь шириной b = 1,5 мм. Магнитная проницаемость железа для данных условий μ = 500. Определить при силе тока через обмотку I = 4 А: 1) напряженность Н магнитного поля в железе; 2) напряженность Н₀ магнитного поля в прорези.

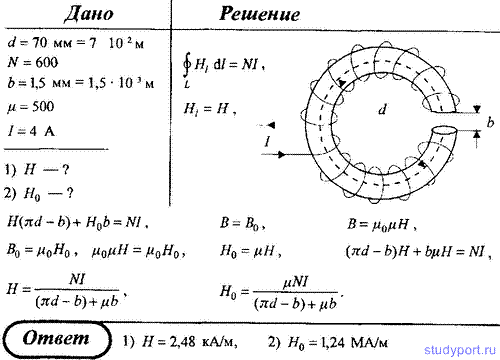
230. Длинный цилиндрический конденсатор заряжается от источника ЭДС. Пренебрегая краевыми эффектами, докажите, что ток смещения в диэлектрике, заполняющем пространство между обкладками конденсатора, равен току в цепи источника ЭДС.

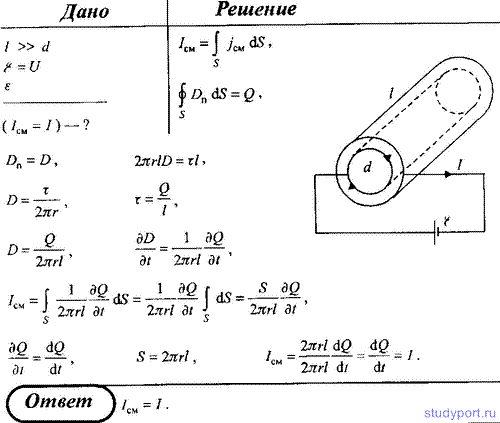
234. Докажите с помощью одного из уравнений Максвелла, что переменное во времени магнитное поле не может существовать без электрического поля.

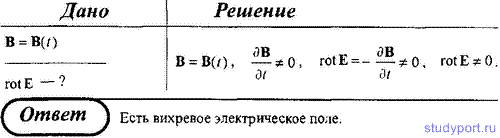
235. Докажите, что уравнения Максвелла rotE = -δB/dt и divB = 0 совместимы, т. е. первое из них не противоречит второму.

236. Ток, проходящий по обмотке длинного прямого соленоида радиусом изменяют так, что магнитное поле внутри соленоида растет со временем по закону В = At², где А — некоторая постоянная. Определите плотность тока смещения как функцию расстояния r от оси соленоида. Постройте график зависимости j_см(r).

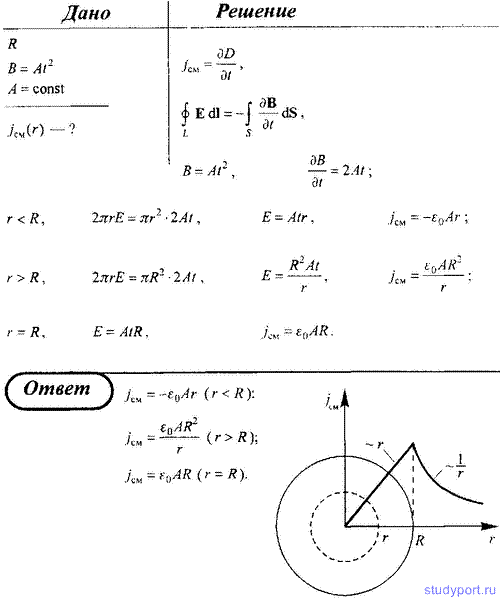
237. В физике известно так называемое уравнение непрерывности, выражающее закон сохранения заряда. Докажите, что уравнения Максвелла содержат это уравнение. Выведите дифференциальную форму уравнения непрерывности.

238. Определите силу тока смещения между квадратными пластинами конденсатора со стороной 5 см, если напряженность электрического поля изменяется со скоростью 4,52 МВ/(м*с).