Страница 1 из 4 В
задачах данного раздела необходимо, прежде чем приступать к числовым
расчетам, представить все величины в единицах системы СИ. Если в задаче
приведена графическая зависимость нескольких величин от какой-либо одной
и при этом все кривые изображены на одном графике, то по оси у задаются
условные единицы.
1.1. Первую половину времени своего движения автомобиль двигался со скоростью v1 = 80 км/ч, а вторую половину време — со скоростью v2 = 40 км/ч. Какова средняя скорость v движения автомобиля?
Решение:
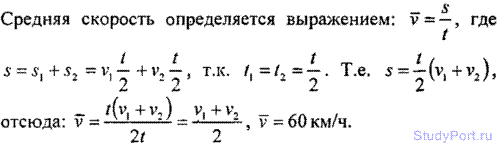
1.2. Первую половину своего пути автомобиль двигался со скоростью v1 = 80 км/ч, а вторую половину пути - со скоростью v2 = 40 км/ч. Какова средняя скорость v движения автомобиля?
Решение:

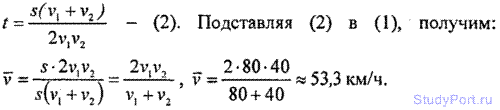
1.3. Пароход идет по реке от пункта А до пункта В со скоростью v1 =10 км/ч, а обратно - со скоростью v2 =16 км/ч.
Найти среднюю скорость v парохода и скорость и течения реки.
Решение:
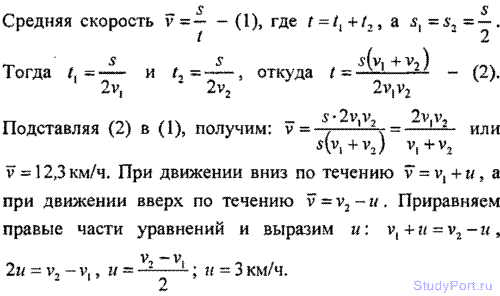
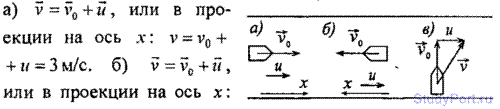
1.4. Найти скорость v относительно берега реки: а) лодки, идущей по
течению; б) лодки, идущей против течения; в) лодки, идущей под углом а =
90° к течению. Скорость течения реки и -1 м/с, скорость лодки
относительно воды v0 = 2 м/с.
Решение:
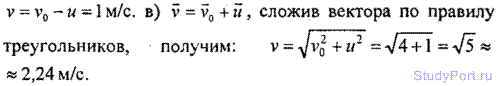
1.5. Самолет летит относительно воздуха со скоростью v0 =
800 км/ч. Ветер дует с запада на восток со скоростью и = 15 м/с. С какой
скоростью v самолет будет двигаться относительно земли и под каким
углом а к меридиану надо держать курс, чтобы перемещение было: а) на юг;
б) на север; в) на запад; г) на восток?
Решение:

1.6. Самолет летит от пункта А до пункта В, расположенного на
расстоянии l = 300 км к востоку. Найти продолжительность t полета, если:
а) ветра нет; б) ветер дует с юга на север; в) ветер дует с запада на
восток. Скорость ветра и -20 м/с, скорость самолета относительно воздуха
v0 = 600 км/ч?
Решение:
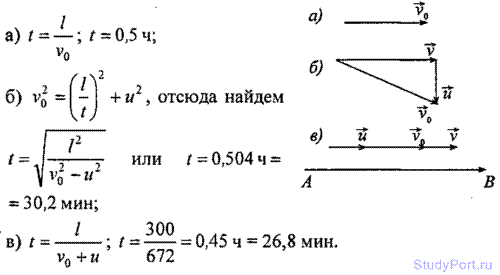
1.7. Лодка движется перпендикулярно к берегу со скоростью v = 7,2
км/ч. Течение относит ее на расстояние l = 150 м вниз по реке. Найти
скорость и течения реки и время t, затраченное на переправу через реку.
Ширина реки L = 0,5 км.
Решение:

1.8. Тело, брошенное вертикально вверх, вернулось на землю через время t = 3 с. Какова была начальная скорость v0 тела и на какую высоту h оно поднялось?
Решение:
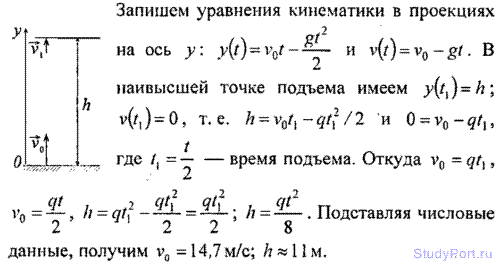
1.9. Камень бросили вертикально вверх на высоту h0 = 10м.
Через какое время t он упадет на землю? На какую высоту h поднимется
камень, если начальную скорость камня увеличить вдвое?
Решение:

1.10. С аэростата, находящегося на высоте h = 300 м, упал камень.
Через какое время t камень достигнет земли, если: а) аэростат
поднимается со скоростью v = 5 м/с; б) аэростат опускается со скоростью v
= 5 м/с; в) аэростат неподвижен?
Решение:


1.11. Тело брошено вертикально вверх с начальной скоростью v0 = 9,8 м/с. Построить график зависимости высоты h и скорости v от времени t для интервала 0 < t < 2 с через 0,2с.
Решение:

1.12. Тело падает с высоты h = 19,6 м с начальной скоростью v0 = 0. Какой путь пройдет тело за первую и последнюю 0,1с своего движения?
Решение:

1.13. Тело падает с высоты h = 19,6 м с начальной скоростью v0 = 0. За какое время тело пройдет первый и последний 1 м своего пути?
Решение:

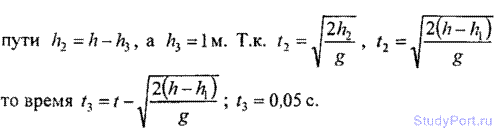
1.14. Свободно падающее тело в последнюю секунду движения проходит
половину всего пути. С какой высоты h падает тело и каково время t его
падения?
Решение:

1.15. Тело 1 орошено вертикально вверх с начальной скоростью v0,
тело 2 падает с высоты h без начальной скорости. Найти зависимость
расстояния l между телами 1 и 2 от времени t, если известно, что тела
начали двигаться одновременно.
Решение:
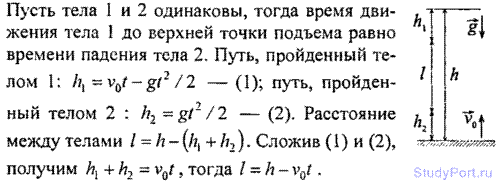
1.16. Расстояние между двумя станциями метрополитена l = 1,5 км.
Первую половину этого расстояния поезд проходит равноускоренно, вторую —
равнозамедленно с тем же по моду ускорением. Максимальная скорость
поезда v = 50 км/ч. Най ускорение a и время t движения поезда между
станциями.
Решение:

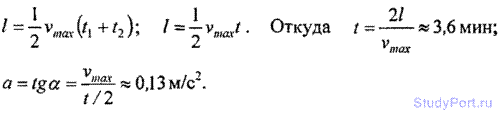
1.17. Поезд движется со скоростью у0=36км/ч. Если
выключить ток, то поезд, двигаясь равнозамедленно, остановит через время
t = 20 с. Каково ускорение а поезда? На каком расстоянии s до остановки
надо выключить ток?
Решение:
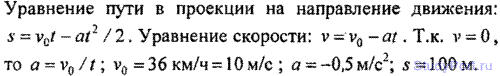
1.18. Поезд, двигаясь равнозамедленио, в течение времени t = 1 мин уменьшает свою скорость от v1 = 40 км/ч до v2 = 28 км/ч. Найти ускорение а поезда и расстояние s, пройденное им за время торможения.
Решение:
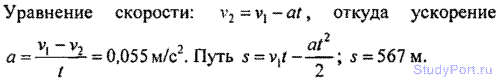
1.19. Поезд движется равнозамедленио, имея начальную скорость v0 = 54 км/ч и ускорение а = -0,5 м/с2. Через какое время t и на каком расстоянии s от начала торможения поезд остановится?
Решение:

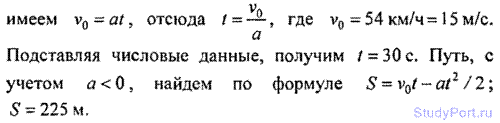
1.20. Тело 1 движется равноускоренно, имея начальную скорость v10 и ускорение а1. Одновременно с телом 1 начинает двигаться равнозамедленио тело 2, имея начальную скорость v20 и ускорение а2. Через какое время t после начала движения оба тела будут иметь одинаковую скорость?
Решение:
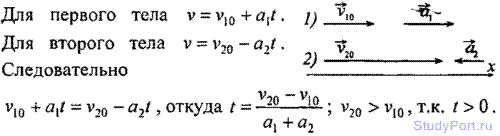
1.21. Тело 1 движется равноускоренно, имея начальную скорость v10=2m/c
и ускорение а. Через время t = 10с после начала движения тела 1 из этой
же точки начинает двигаться равноускоренно тело 2, имея начальную
скорость v20 =12 м/с и то же ускорение а. Найти ускорение a, при котором тело 2 сможет догнать тело 1.
Решение:

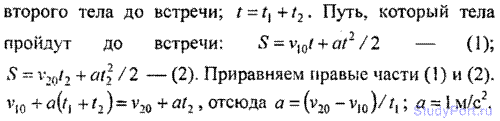
1.22. Зависимость пройденного телом пути s от времени t дается уравнением s = At - Br2 + Сt3, где А = 2 м/с, 5 = 3м/с2 и С = 4м/с3.
Найти: а) зависимость скорости v и ускорения а от времени t; б)
расстояние s, пройденное телом, скорость v и ускорение a тела через
время t = 2 с после начала движения. Построить график зависимости пути
s, скорости v и ускорения a от времени t для интервала 0 < t < 3 с
через 0,5с.
Решение:
1.23. Зависимость пройденного телом пути s от времени t дается уравнением 5 = А -Bt + Ct2, где а = 6м, 5 = 3м/с и С = 2 м/с2.
Найти среднюю скорость v и среднее ускорение а тела для интервала
времени l < t < 4 с. Построить график зависимости пути S,
скорости v и ускорения а от времени t для интервала 0 < t < 5 с
через 1с.
Решение:
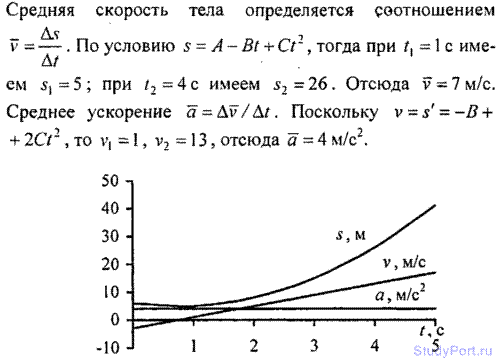
1.24. Зависимость пройденного телом пути s от времени t дается уравнением s = A + Bt + Ct2, где A = 3м, B = 2м/с и С = 1 м/с2. Найти среднюю скорость v и среднее ускорение а тела за первую, вторую и третью секунды его движения.
Решение:
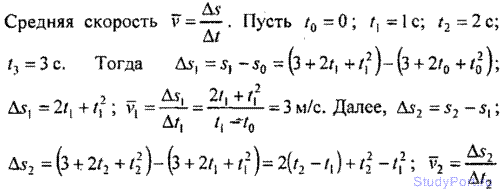
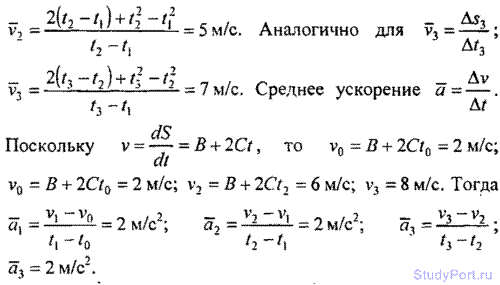
1.25. Зависимость пройденного телом пути s от времени / дается уравнением s = А + Bt + Ct2 + Dt3, где С = 0,14 м/с2 и D = 0,01m/c3. Через какое время / тело будет иметь ускорение а = 1 м/с2? Найти среднее ускорение а тела за этот промежуток времени.
Решение:
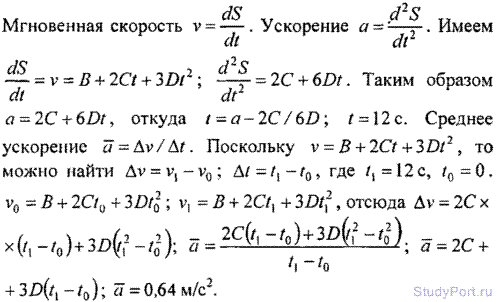
1.26. С башни высотой h = 25м горизонтально брошен ка со скоростью vt=15m/c.
Какое время t камень будет в движении? На каком расстоянии l от
основания башни он упа на землю? С какой скоростью v он упадет на землю?
Какой угол ф составит траектория камня с горизонтом в точке его па на
землю?
Решение:

1.27. Камень, брошенный горизонтально, упал на землю через время t =
0,5 с на расстоянии l = 5 м по горизонтали от места бросания. С какой
высоты h брошен камень? С какой скоростью vx он брошен? С
какой скоростью он упадет на землю? Какой угол ф составит траектория
камня с горизонтом в точке его падения на землю?
Решение:
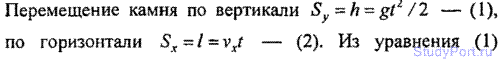

1.28. Мяч, брошенный горизонтально, ударяется о стенку, находящуюся
на расстоянии l = 5 м от места бросания. Высота места удара мяча о
стенку на h = 1 м меньше высоты h, с кото брошен мяч. С какой скоростью vx брошен мяч? Под каким углом ф мяч подлетает к поверхности стенки?
Решение:

1.29. Камень, брошенный горизонтально, через время t = 0,5 с после
начала движения имел скорость v, в 1,5 раза большую скорости vx в момент бросания. С какой скоростью vx был брошен камень?
Решение:

1.30. Камень брошен горизонтально со скоростью vy = 15 м/с. Найти нормальное ап и тангенциальное аr ускорения камня че время t = 1 с после начала движения.
Решение:

1.31. Камень брошен горизонтально со скоростью vx = 10 м/с.
Найти радиус кривизны R траектории камня через время t = 3 с после начала движения.
Решение:

1.32. Мяч брошен со скоростью v0 = 10 м/с под углом
а = 40° к горизонту. На какую высоту h поднимется мяч? На каком
расстоянии l от места бросания он упадет на землю? Какое время t он
будет в движении?
Решение:
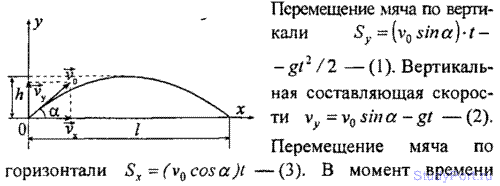
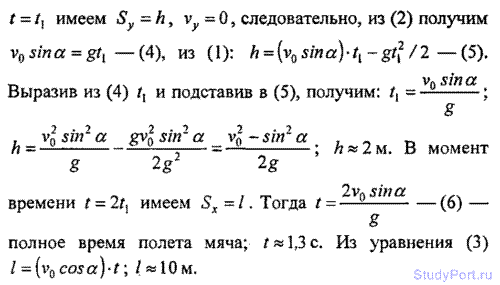
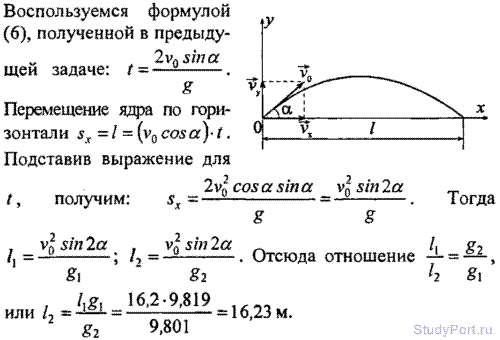
1.33. На спортивных состязаниях в Ленинграде спортсмен толкнул ядро на расстояние l1 = 16,2 м. На какое расстояние l2
полетит такое же ядро в Ташкенте при той же начальной скорости и при
том же угле наклона ее к горизонту? Ускорение свободного падения в
Ленинграде g1 =9,819 м/с2, в Ташкенте
g2 =9,801 м/с2.
Решение:
1.34. Тело брошено со скоростью v0 под углом к горизонту. Время полета l = 2,2 с. На какую высоту h поднимется тело?
Решение:

1.35. Камень, брошенный со скоростью v0 = 12 м/с под углом
а = 45° к горизонту, упал на землю на расстоянии l от места бросания. С
какой высоты h надо бросить камень в горизонтальном направлении, чтобы
при той же начальной скорости v0 он упал на то же место?
Решение:

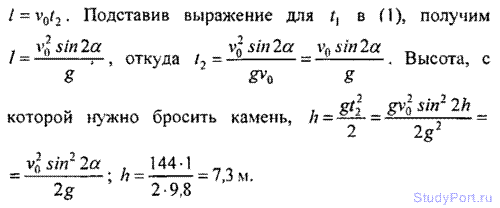
1.36. Тело брошено со скоростью v0= 14,7 м/с под углом а = 30° к горизонту. Найти нормальное аn и тангенциальное аt ускорения тела через время t = 1,25 с после начала движения.
Решение:

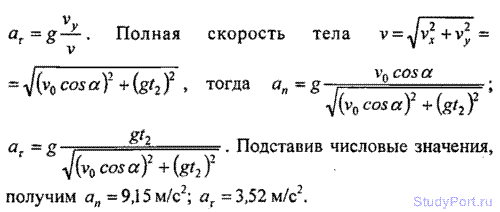
1.37. Тело брошено со скоростью v0=10m/c под углом а = 45° к горизонту. Найти радиус кривизны R траектории тела через время t = 1 с после начала движения.
Решение:

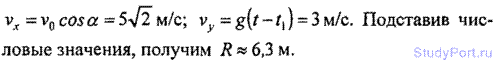
1.38. Тело брошено со скоростью v0 под углом а к горизонту. Найти скорость v0 и угол а, если известно, что высота подъема тела А = 3м и радиус кривизны траектории тела в верхней точке траектории R = 3 м.
Решение:
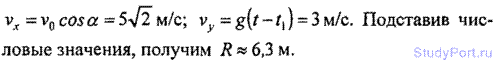
1.39. С башни высотой h0 =25м брошен камень со скоро v0
= 15 м/с под углом а =30° к горизонту. Какое время t камень будет в
движении? На каком расстоянии l от основания башни он упадет на землю? С
какой скоростью v он упадет на землю? Какой угол ф составит траектория
камня с горизонтом в точке его падения на землю?
Решение:


1.40. Мяч, брошенный со скоростью v0=10m/c под углом а =
45° к горизонту, ударяется о стенку, находящуюся на рас l = 3 м от места
бросания. Когда происходит удар мяча о стенку (при подъеме мяча или при
его опускании)? На какой высоте h мяч ударит о стенку (считая от
высоты, с которой брошен мяч)? Найти скорость v мяча в момент удара.
Решение:

|