12.1. Написать уравнение гармонического колебательного движения с амплитудой A = 5см, если за время t = 1мин совершается 150 колебаний и начальная фаза колебаний φ = P/4. Начертить график этого движения.

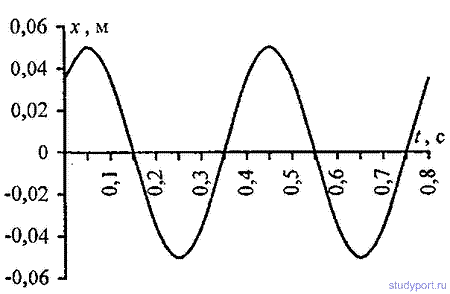
12.2. Написать уравнение гармонического колебательного движения с амплитудой A = 0,1M, периодом T = 4с и начальной фазой φ = 0.

12.3. Написать уравнение гармонического колебательного движения с амплитудой A = 50мм, периодом T = 4с и начальной фазой φ = P/4 . Найти смещение х колеблющейся точки от положения равновесия при t = 0 и t= 1,5 с. Начертить график этого движения.

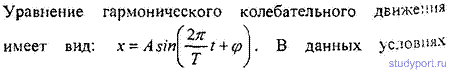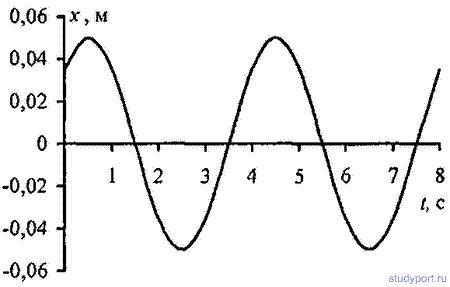
12.4. Написать уравнение гармонического колебательного движения с амплитудой А = 5 см и периодом Т = 8 с, если начальная фаза φколебаний равна: а) 0; б) P/2; ^в) P ^г) 3P/2 д) 2P. Начертить график этого движения во всех случаях.

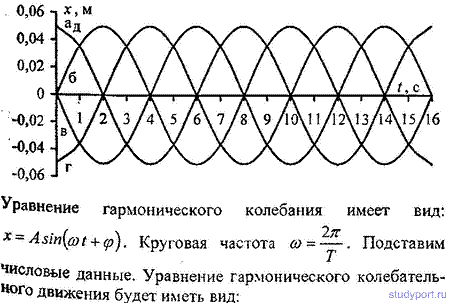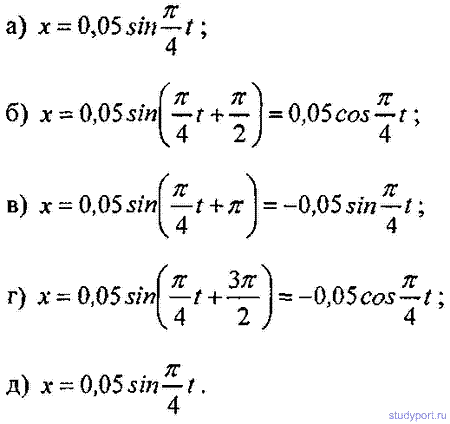
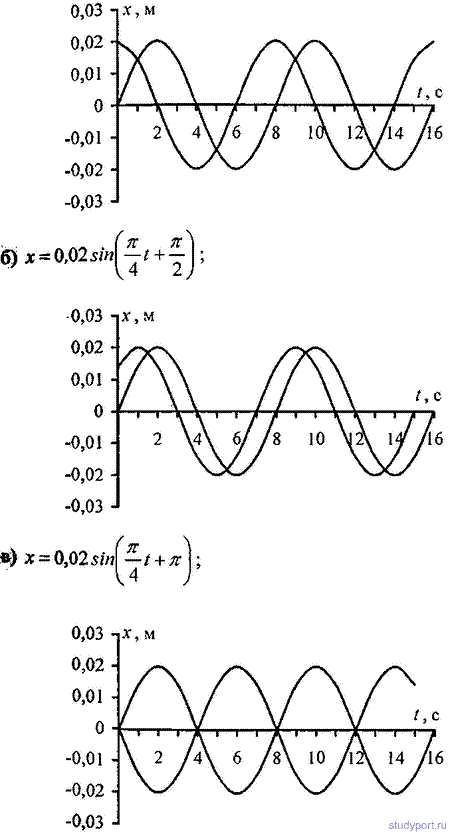
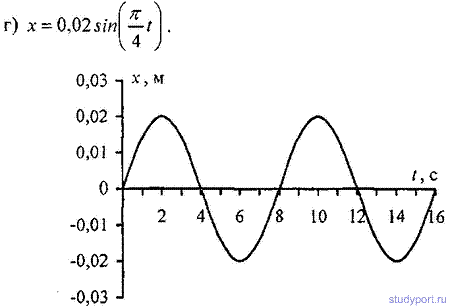
12.5. Начертить на одном графике два гармонических колебания с одинаковыми амплитудами A₁ = А₂ = 2 см и одинаковыми периодами T₁ = Т₂ = 8 с, но имеющие разность фаз φ₂-φ₁,

равную: а) P/4; о) P/2; в) P; г) 2P.

12.6. Через какое время от начала движения точка, совершающая гармоническое колебание, сместится от положения равновесия на половину амплитуды? Период колебаний Т = 24 с, начальная фаза φ = 0.

12.7. Начальная фаза гармонического колебания φ= 0. Через какую долю периода скорость точки будет равна половине ее максимальной скорости?

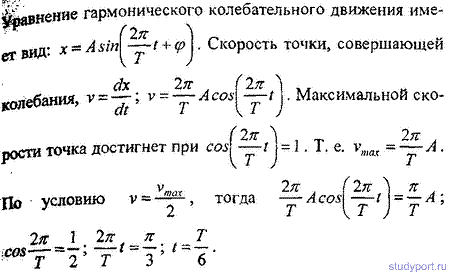
12.8. Через какое время от начала движения точка, совершающая колебательное движение по уравнению х = 7 sinP/2*t, проходит путь от положения равновесия до максимального смещения?

12.9. Амплитуда гармонического колебания /4 = 5 см, период Г = 4с. Найти максимальную скорость v_mat колеблющейся _Точ кн и ее максимальное ускорение a_тах.

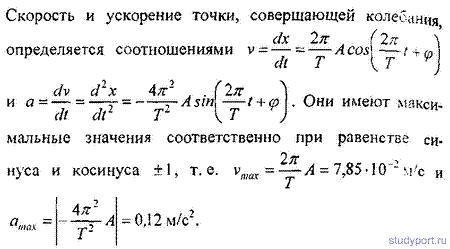
12.10. Уравнение движения точки дано в виде х = 2si>i^( ^{+ СМ}' ^^{аити пе}Р^П0'^а колебаний Г, максимальную скорость \>_тах и максимальное ускорение a_та точки.

t2.ll. Уравнение движения точки дано в виде x = sin—t. > 6

ahftm моменты времени /, в которые достигаются максималь-

^шГскорость и максимальное ускорение.

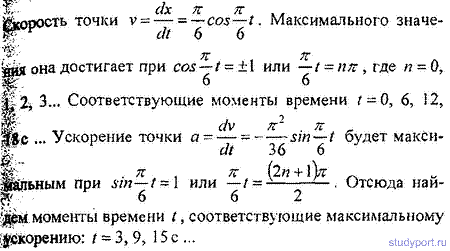
12.12. Точка совершает гармоническое колебание. Период колебаний Т = 2 с, амплитуда А = 50 мм, начальная фаза <р = 0. .$айти скорость v точки в момент времени, когда смешение точ-^;виот положения равновесия х = 25 мм.

12.13. Написать уравнение гармонического колебательного ^юкения, если максимальное ускорение точки a_тах =49,3 см/с²,

период колебаний T = 2с и смещение точки от положения равновесия в начальный момент времени х₀ = 25 мм.

12.14. Начальная фаза гармонического колебания φ= 0 . При смещении точки от положения равновесия х₁ = 2,4 см скорость точки v₁ = 3 см/с, а при смещении x₂ = 2,8 см ее скорость v₂ = 2 см/с. Найти амплитуду А и период Т этого колебания.

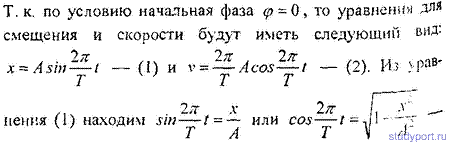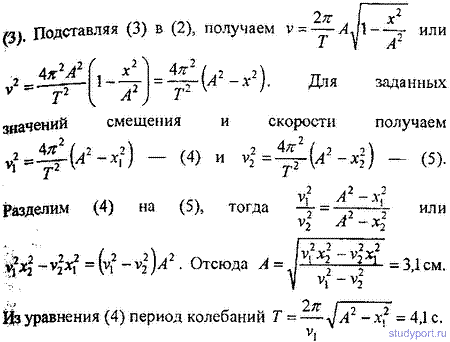
12.15. Уравнение колебания материальной точки массой

m=16г имеет вид х = 0,1 sin(P/8*t+P/4)- Построить график

зависимости от времени t ( в пределах одного периода) силы F, действующей на точку. Найти максимальную силу F_max.

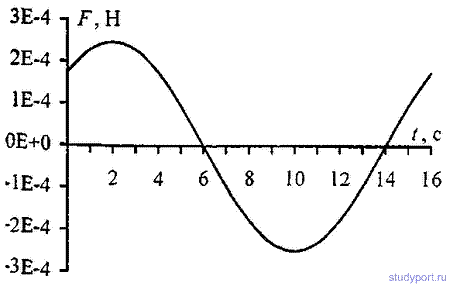
12.16. Уравнение колебаний материальной точки массой

m=10г имеет вид x=5sin(P/5*t+P/4) см. Найти максимальную силу F_mix, действующую на точку, и полную энергию Wколеблющейся точки.

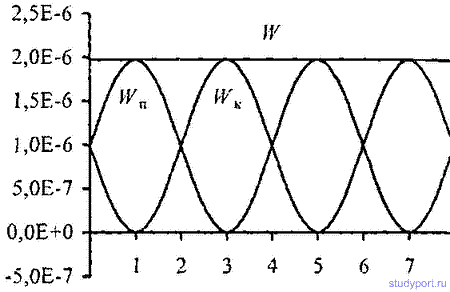
12.17. Уравнение колебания материальной точки массой

m=16г имеет вид х = 2sin(P/4*t+P/4) см. Построить график зависимости от времени t ( в пределах одного периода) кинетической W_K, потенциальной W„ и полной W энергии ТОЧКИ.

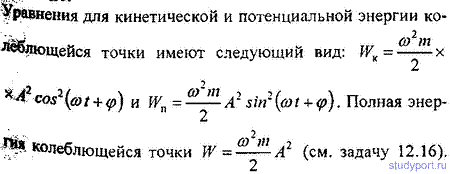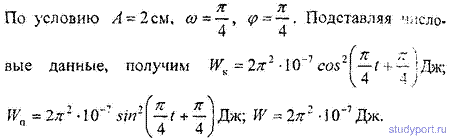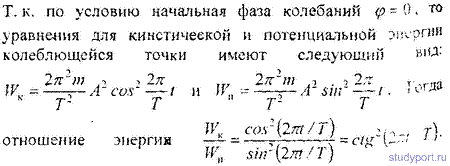
12.18. Найти отношение кинетической W_K энергии точки, совершающей гармоническое колебание, к ее потенциальной энергии W_n для моментов времени: a) t = T/12; б) t=T/8 в) t= T/6 . Начальная фаза колебаний φ= 0.

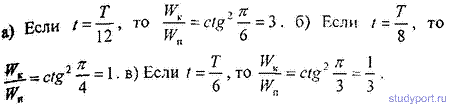
12.19. Найти отношение кинетической энергии W_K точки, совершающей гармоническое колебание, к ее потенциальной энергии W_a для моментов, когда смещение точки от положения равновесия составляет: а) х = A/4; б) х = A/2 ; в) х = А , где А — амплитуда колебаний.

12.20. Полная энергия тела, совершающего гармоническое колебательное движение, W=30 мкДж; максимальная сила, действующая на тело, F_mm. = 1,5 мН. Написать уравнение движения этого тела, если период колебаний Т = 2с и начальная фаза φ=P/3

12.21. Амплитуда гармонических колебаний материальной точки А = 2 см, полная энергия колебаний W = 0,3 мкДж. При каком смещении x от положения равновесия на колеблющуюся точку действует сила F = 22,5 мкН?

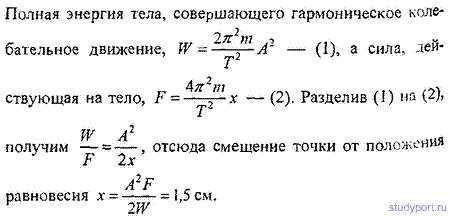
12 22. Шарик, подвешенный на нити длиной l = 2 м, отклоняют на угол a = 4° и наблюдают его колебания. Полагая колебаниянезатухающими гармоническими, найти скорость шарика при прохождении им положения равновесия. Проверить полученное решение, найдя скорость шарика при прохождении им положения равновесия из уравнений механики.

12.23. К пружине подвешен груз массой m = 10кг. Зная, что пружина под влиянием силы F = 9,8 Н растягивается на l = 1.5 см, найти период Т вертикальных колебаний груза.

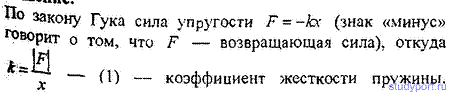
12.24. К пружине подвешен груз. Максимальная кинетическая энергия колебаний груза W_Kma = 1 Дж. Амплитуда колебаний A = 5 см. Найти жесткость к пружины.

12.25. Как изменится период вертикальных колебаний груза, висящего на двух пружинах, если от последовательного соединения пружин перейти к параллельному их соединению?

12.26. Медный шарик, подвешенный к пружине, совершает вертикальные колебания. Как изменится период колебаний, если к пружине подвесить вместо медного шарика алюминиевый такого же радиуса?

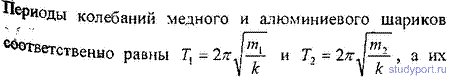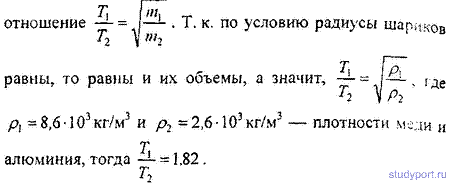
12.27. К пружине подвешена чашка весов с гирями. При эгом период вертикальных колебаний T₁ = 0,5 с. После того как на чашку весов положили еще добавочные гири, период вертикальных колебаний стал равным T₂ =0,6 с. На сколько удлинилась пружина от прибавления этого добавочного груза?

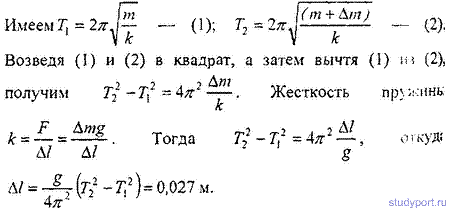
12.28. К резиновому шнуру длиной l = 40см и радиусом r = 1мм подвешена гиря массой m = 0,5 кг. Зная, что модуль Юнга резины Е = 3 МН/м², найти период Т вертикальных колебаний гири. Указание: учесть, что жесткость kрезины связана с модулем Юнга Е соотношением к = SE/l, где S - площадь поперечного сечения резины, l — ее длина.

12.29. Ареометр массой m= 0,2 кг плавает в жидкости. Если погрузить его немного в жидкость и отпустить, то он начнет совершать колебания с периодом Т = 3,4 с. Считая колебания незатухающими, найти плотность жидкости p, в которой плавает ареометр. Диаметр вертикальной цилиндрической трубки ареометра d = 1 см.

12.30. Написать уравнение движения, получающегося в результате сложения двух одинаково направленных гармонических колебательных движений с одинаковым периодом T = 8с и одинаковой амплитудой А = 0,02 м. Разность фаз между этими колебаниями φ₂ - φ₁ = P/4 . Начальная фаза одного из этих колебаний равна нулю.

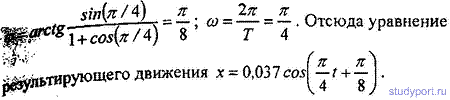
12.31. Найти амплитуду А и начальную фазу φгармонического колебания, полученного от сложения одинаково направленных колебаний, данных уравнениями х₁ = 0,02 х

2.32. В результате сложения двух одинаково направленных гармонических колебаний с одинаковыми амплитудами и одинаковыми периодами получается результирующее колебание с тем же периодом и той же амплитудой. Найти разность фаз φ₂-φ₁ складываемых колебаний.

12.33. Найти амплитуду А и начальную фазу φгармонического колебания, полученного от сложения одинаково направленных колебаний, данных уравнениями x₁ = 4 sinPсм и х₂ = sin(Pt+P/2). Написать уравнение результирующего колебания. Дать векторную диаграмму сложения амплитуд.

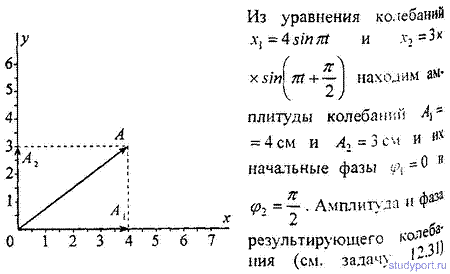
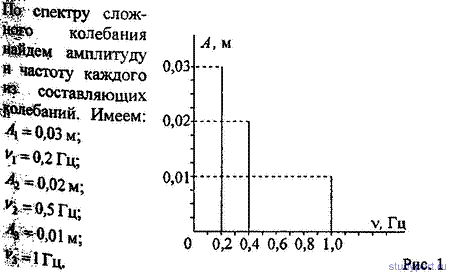
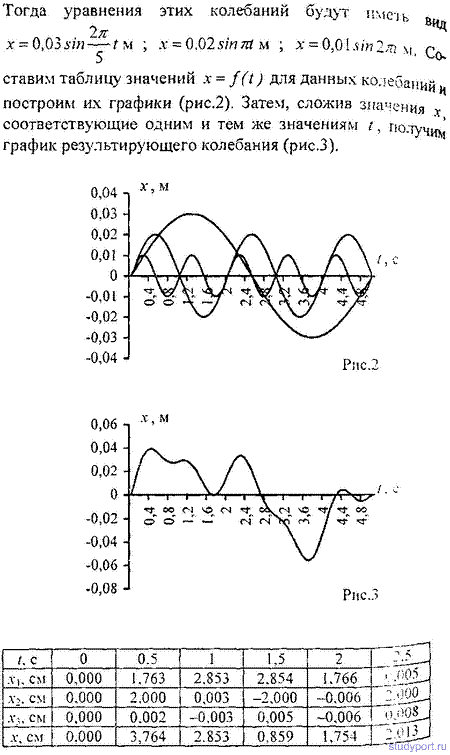
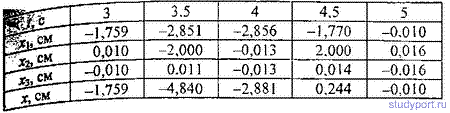
12.34. На рис. 1 дан спектр результирующего колебания. Пользуясь данными этого рисунка, написать уравнения колебаний, из которых составлено результирующее колебание, Начертить график этих колебаний. Принять, что в момент t = 0 разность фаз между этими колебаниями φ₂-φ₁ = 0. Начертить график результирующего колебания.

12.35. Уравнения двух гармонических колебаний имеют вид x₁=3sin 4Pt см и х₂ = 6sin10Pt см. Построить график этих колебаний. Сложив графически эти колебания, построить график результирующего колебания. Начертить спектр результирующего колебания.

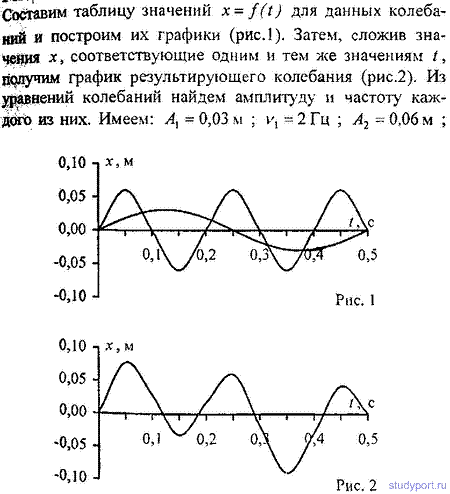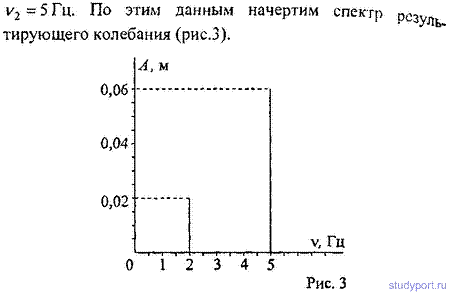
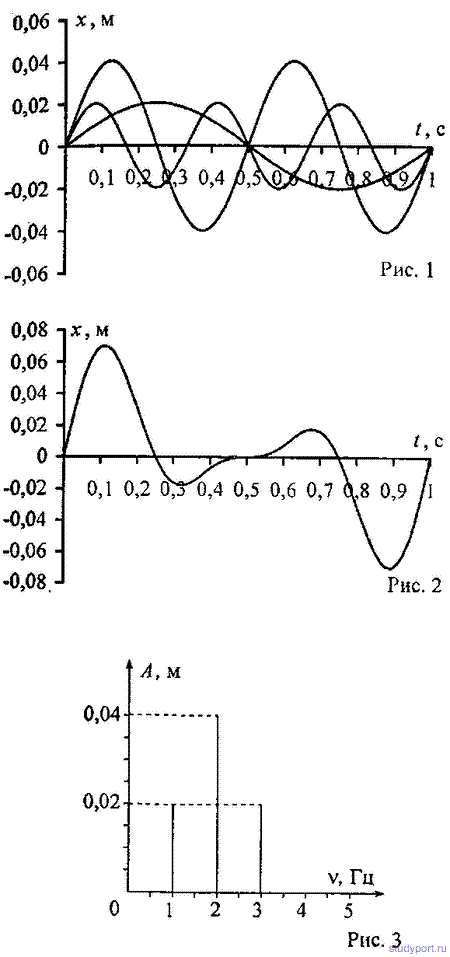
12.36. Уравнение колебаний имеет вид х = Asin2Pv₁t, причем амплитуда А изменяется со временем по закону А = A₀(1 + cos2Pv₂t). Из каких гармонических колебаний состоит колебание? Построить график слагаемых и результирующего колебаний для А₀ = 4 см, v₁ = 2 Гц, v₂ = 1 Гц. Начертить спектр результирующего колебания.

12.37. Написать уравнение результирующего колебания получающегося в результате сложения двух взаимно перпендикулярных колебаний с одинаковой частотой v₁ = v₂ = 5 Гц одинаковой начальной фазой φ₁=φ₂=P/3. Амплитуды колебаний равны A₁ = 0,10 м и А_г = 0,05 м.

12.38. Точка участвует в двух колебаниях одинакового пер" ода с одинаковыми начальными фазами. Амплитуды кол-бан'¹¹¹ равны А, =3см и А, =4 см. Найти амплитуду А р->> льтирУ юшего ко.теоания, если колсоання совершаются: а) в ■ ^iU-правлении; б) в двух взаимно перпендикулярных паи.:л^;:ях-

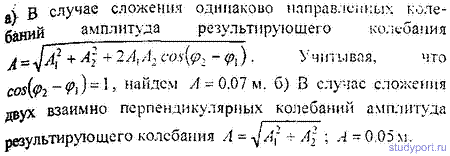
12.39. Точка участвует в двух взаимно перпендикулярных колебаниях х = 2sinwt м и у = 2 cos wt м. Найти траекторию результирующего движения точки.

12.40. Точка участвует в двух взаимно перпендикулярных колебания x=cosPtи y = cos P/2 t. Найти траекторию результиующего движения точки и начертить ее с нанесением масштаба.

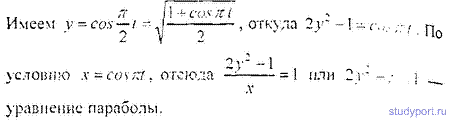
12.41. Точка участвует в двух взаимно перпендикулярных колебаниях x = sinPt и y = 2sin(Pt+P/2). Найти траекторию результирующего движения точки.

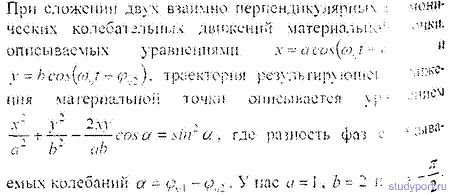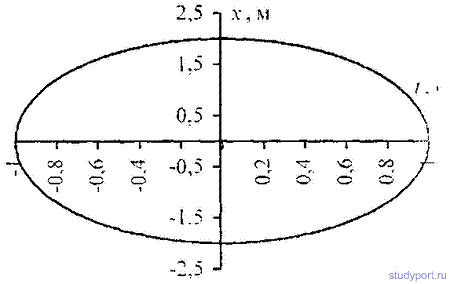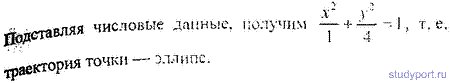
12 42. Точка участвует в двух взаимно перпендикулярных колебаниях х = sinPt a y = 4sin(Pt + P). Найти траекторию результирующего движения точки и начертить ее с нанесением масштаба.

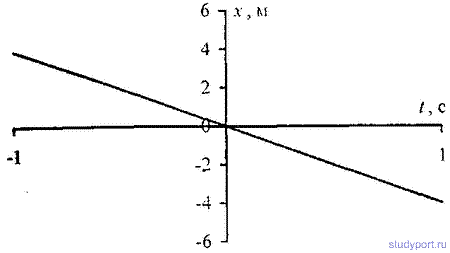
12.43. Период затухающих колебаний T = 4с; логарифмический декремент затухания N = 1.6; начальная фаза φ = 0. При t=T/4 смещение точки x = 4,5 см. Написать уравнение движения

этого колебания. Построить график этого колебания в пределах двух периодов.

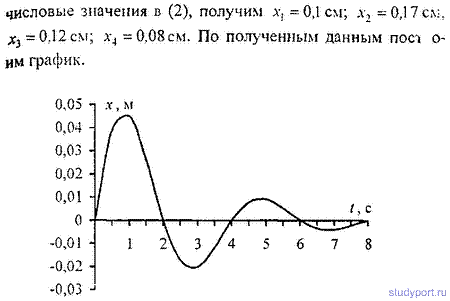
12.44. Построить график затухающего колебания, данного

уравнением x=5e^-0,1tsinP/4t м.

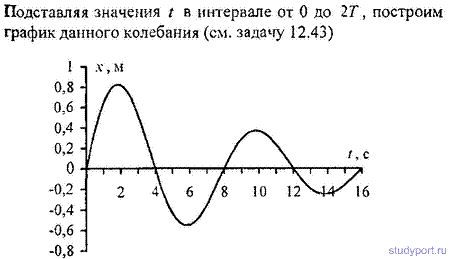
12.45. Уравнение затухающих колебаний дано в виде x=5e^-0,25tsinP/2tм. Найти скорость v колеблющейся точки в моменты времени t, равные: 0, T, 2T, 3Т и 4T,

12.46. Логарифмический декремент затухания математического маятника N = 0.2. Во сколько раз уменьшится амплитуда колебаний за одно полное колебание маятника?

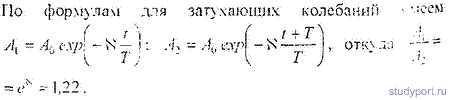
12.47. Найти логарифмический декремент затухания математического маятника, если за время t = 1мин амплитуда колебаний уменьшилась в 2 раза. Длина маятника l= 1м.

12.48. Математический маятник длиной l = 24,7 см совершает затухающие колебания. Через какое время t энергия колебаний маятника уменьшится в 9,4 раза? Задачу решить при значении логарифмического декремента затухания: а) N = 0,01; б) N = 1.

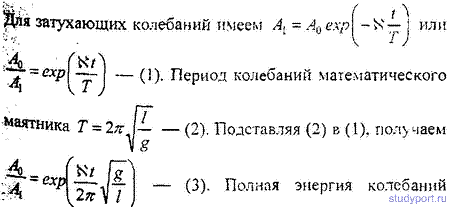
12.49. Математический маятник совершает затухающие колебания с логарифмическим декрементом затухания N = 0,2 . Во сколько раз уменьшится полное ускорение маятника в его крайнем положении за одно колебание?

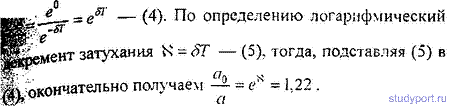
12.50. Амплитуда затухающих колебаний математического маятника за время t = 1 мин уменьшилась вдвое. Во сколько раз уменьшится амплитуда за время t = 3 мин?

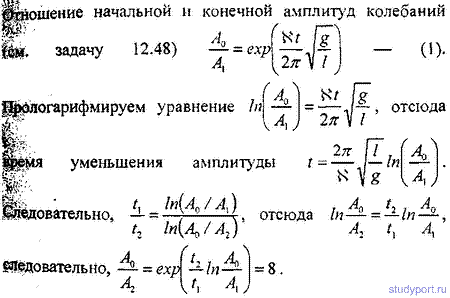
12.51. Математический маятник длиной l = 0,5м, выведенный из положения равновесия, отклонился при первом колебании на х₁ = 5 см, а при втором ( в ту же сторону) — на x₂ = 4см. Найти время релаксации t, т. е. время, в течение которого амплитуда колебаний уменьшится в е раз, где е — основание натуральных логарифмов.

12.52. К вертикально висящей пружине подвешивают груз. При этом пружина удлиняется на dl = 9,8см. Оттягивая этот груз вниз и отпуская его, заставляют груз совершать колебания. Каким должен быть коэффициент затухания δ, чтобы: а) колебания прекратились через время t = 10 с (считать условно, что колебания прекратились, если их амплитуда упала до 1% от начальной); б) груз возвращается в положение равновесия апериодически; в) логарифмический декремент затухания колебаний был равным N = 6 ?

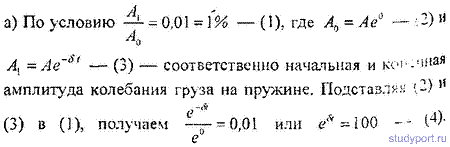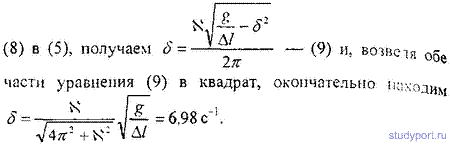
12.53. Тело массой m = 10 г совершает затухающие колебания с максимальной амплитудой A_max = 7см, начальной фазой φ = о и коэффициентом затухания δ = 1,6 см^-1. На это тело начала действовать внешняя периодическая сила F, под действием которой установились вынужденные колебания. Уравнение вынужденных колебаний имеет вид х = 5sin(10Pt-3P/4) см. Найти (с числовыми коэффициентами) уравнение собственных колебаний и уравнение внешней периодической силы.

12.54. Гиря массой m = 0,2 кг, висящая на вертикальной пружине, совершает затухающие колебания с коэффициентом затухания δ= 0,75 см^-1. Жесткость пружины k = 0,5кН/м. Начертить зависимость амплитуды А вынужденных колебаний гирьки от частоты внешней периодической силы, если известно, что максимальное значение внешней силы F₀ = 0,98 Н. Для построения .трафика найти значение А для частот: w= 0, w= 0,5, w = 0,75, w = w₀, w = w=1,5w₀ и w = 2w₀, где w₀— частота собственных колебаний подвешенной гири.

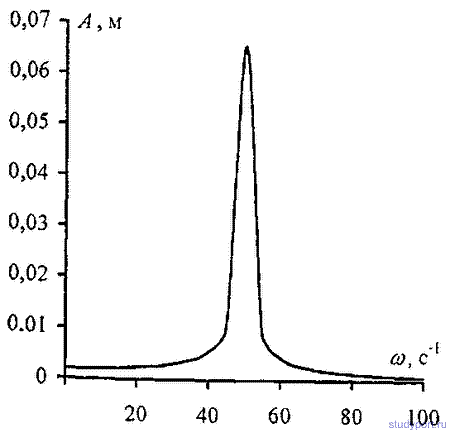
12.55. По грунтовой дороге прошел трактор, оставив следы в виде ряда углублений, находящихся на расстоянии l = 30 см друг от друга. По этой дороге покатили детскую коляску, имеющую две одинаковые рессоры, каждая из которых прогибается на x₀ = 2 см под действием груза массой m₀ = 1 кг. С какой скоростью v катили коляску, если от толчков на углублениях она, попав в резонанс, начала сильно раскачиваться? Масса коляски M= 10 кг.

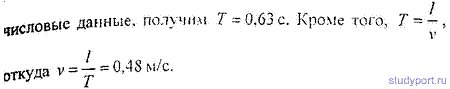
12.56. Найти длину волны λ колебания, период которого T = 10^-14 с. Скорость распространения колебаний с = 3 * 10⁸ м с.

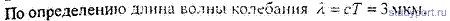
12.57. Звуковые колебания, имеющие частоту v = 500 Гц и амплитуду A =0.25 мм. распространяются в воздухе. Длина волны λ = 70 см. Найти скорость с распространения колебаний и максимальную скорость V_max частиц воздуха.

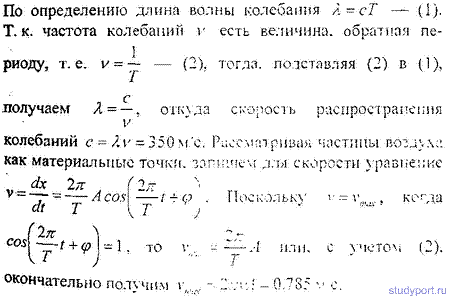
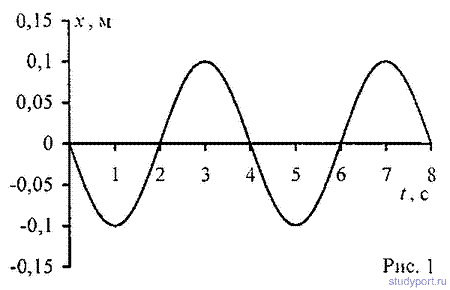
12.58. Уравнение незатухающих колебаний имеет вид

x=10sinP/2*t см. Найти уравнение волны, если скорость распространения колебаний с = 300м*с. Написать и изобразить графически уравнение колебания для точки, отстоящей на расстоянии

l = 600 м от источника колебаний. Написать и изобразить графически уравнение колебания для точек волны в момент времени t= 4 с после начала колебаний.

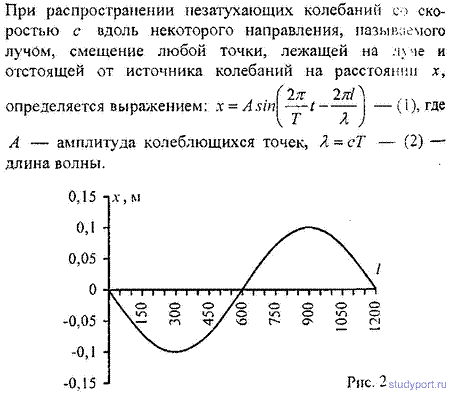
12.59. Уравнение незатухающих колебаний имеет вид x = 4sin600Pt см. Найти смещение x от положения равновесия

точки, находящейся на расстоянии l = 75 см от источника колебаний, для момента времени t = 0,01 с после начала колебаний. Скорость распространения колебаний с = 300 м/с.

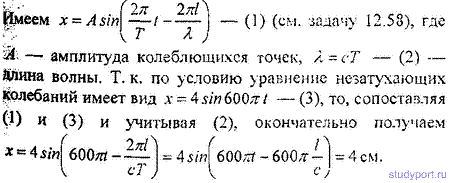
12.60. Уравнение незатухающих колебаний имеет вид x=sin2,5Pt см. Найти смещение х от положения равновесия, скорость v и ускорение a точки, находящейся на расстоянии

l = 20м от источника колебаний, для момента времени t = 1с после начала колебаний. Скорость распространения колебаний с = 100 м*с.

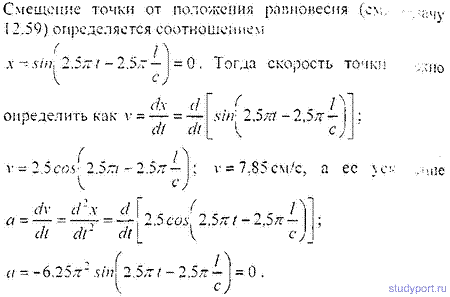
12.61. Найти разность фаз колебаний двух точек, стоящих от источника колебаний на расстояниях l₁ = и l₂ = 16 м. Период колебаний Т = 0,04 с; скорость распространения с = 300 м с.

12.62. Найти разность фаз dφколебаний двух точек, лежащих на луче и отстоящих на расстоянии l = 2м друг от друга, если длина волны λ= 1 м.

12.63. Найти смещение x от положения равновесия точки, отстоящей от источника колебаний на расстоянии l ⁼ λ/12, для момента времени t = T/6 . Амплитуда колебаний А = 0,05 м.

12.64. Смещение от положения равновесия точки, отстоящей источника колебании на расстоянии l = 4см. в момент времени t =T/6 равно половине амплитуды. Найти длину λ ,бегущей волны.

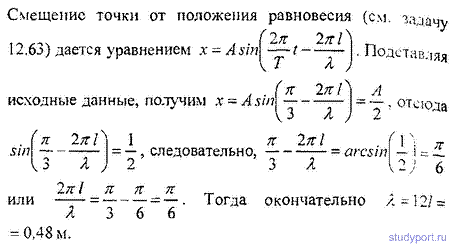
12.65. Найти положение узлов и пучностей и начертить график стоячей волны, если: а) отражение происходит от менее плотной среды; б) отражение происходит от более плотной среды. Длина бегущей волны λ = 12 см.

12.66. Найти длину волны Я колебаний, если расстояние Между первой и четвертой пучностями стоячей волны l = 15 см.