2.80. Пуля, летящая горизонтально, попадает в шар, подвешенный на
невесомом жестком стержне, и застревает в нем. Масса пули в 1000 раз
меньше массы шара. Расстояние от центра шара до точки подвеса стержня l =
1 м. Найти скорость v пули, если известно, что стержень с шаром
отклонился от удара пули на угол а = 10°.
Решение:

2.81. Пуля, летящая горизонтально, попадает в шар, подвешенный на невесомом жестком стержне, и застревает в нем. Масса пули m1 = 5 г, масса шара т2 = 0.5 кг. Скорость пули v1
= 500 м/с. При каком предельном расстоянии l от центра шара до точки
подвеса стержня шар от удара пули поднимется до верхней точки
окружности?
Решение:

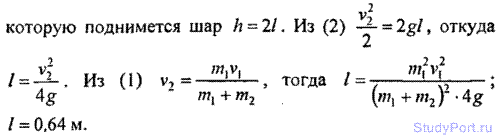
2.82. Деревянным молотком, масса которого т1 = 0,5 кг, ударяют о неподвижную стенку. Скорость молотка в момент удара v1 = 1 м/с. Считая коэффициент восстановления при ударе молотка о стенку k = 0,5, найти количество теплоты Q,
выделившееся при ударе. (Коэффициентом восстановления материала тела
называют отношение скорости после удара к его скорости до удара.)
Решение:
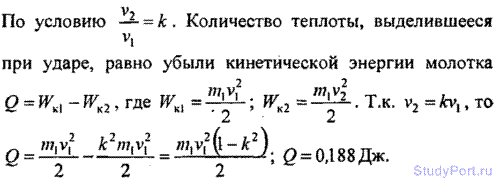
2.83. В условиях предыдущей задачи найти импульс силы Fdt, полученный стенкой за время удара.
Решение:

2.84. Деревянный шарик массой т = 0,1 кг падает с высоты h1 = 2 м. Коэффициент восстановления при ударе шарика о пол к = 0,5. Найти высоту h2 , на которую поднимется шарик после удара о пол, и количество теплоты Q, выделившееся при ударе.
Решение:

2.85. Пластмассовый шарик, падая с высоты h1 = 1 м несколь раз отскакивает от пола. Найти коэффициент восстановления к при ударе шарика о пол, если с момента падения до второго удара о пол прошло время t = 1,3 с.
Решение:
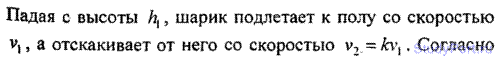

2.86. Стальной шарик, падая с высоты h1 = 1,5 м на стальную плиту, отскакивает от нее со скоростью v2 = 0,75 • v1, где v1— скорость, с которой он подлетает к плите. На какую высоту h2 он поднимется? Какое время t пройдет с момента падения до второго удара о плиту?
Решение:


2.87. Металлический шарик, падая с высоты h1 = 1 м на стальную плиту, отскакивает от нее на высоту h2 =81 см. Найти коэффициент восстановления к при ударе шарика о плиту.
Решение:

2.88. Стальной шарик массой т = 20 г, падая с высоты h1 = 1 м на стальную плиту, отскакивает от нес на высоту h2=81см. Найти импульс силы Fdt, полученный плитой за время удара, и количество теплоты Q, выделившееся при ударе.
Решение:
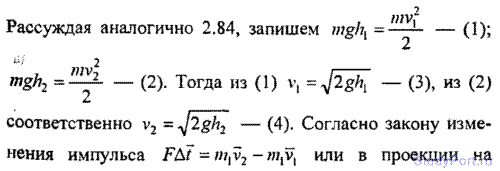

2.89. Движущееся тело массой m1, ударяется о неподвижное тело массой т2. Считая удар неупругим и центральным, найти, какая часть кинетической энергии WKl первого тела переходит при ударе в тепло. Задачу решить сначала в общем виде, а затем рассмотреть случаи: а) m1 = т2; б) m1 = 9т2.
Решение:

2.90. Движущееся тело массой m1 ударяется о неподвижное тело массой т2. Считая удар упругим и центральным, найти, какую часть кинетической энергии Wк] первое тело передает второму при ударе. Задачу решить сначала в общем виде, а затем рассмотреть случаи: а)m1 = m2; б)m1 = 9т2.
Решение:

2.91. Движущееся тело массой т{ ударяется о неподвижное тело массой т2. Каким должно быть отношение масс т{/т2, чтобы при центральном упругом ударе скорость первого тела уменьшилась в 1,5 раза? С какой кинетической энергией W'k2 начинает двигаться при этом второе тело, если первоначальная кинетическая энергия первого тела Жк1 = 1 кДж?
Решение:


2.92. Нейтрон (масса т0) ударяется о неподвижное ядро ато углерода (т = 12т0). Считая удар центральным и упругим, найти, во сколько раз уменьшится кинетическая энергия WK ней при ударе.
Решение:

2,93. Нейтрон (масса т0) ударяется о неподвижное ядро: а) атома углерода (т = 12т0); б) атома урана (m = 235m0). Считая удар центральным и упругим, найти, какую часть скорости v потеряет нейтрон при ударе.
Решение:

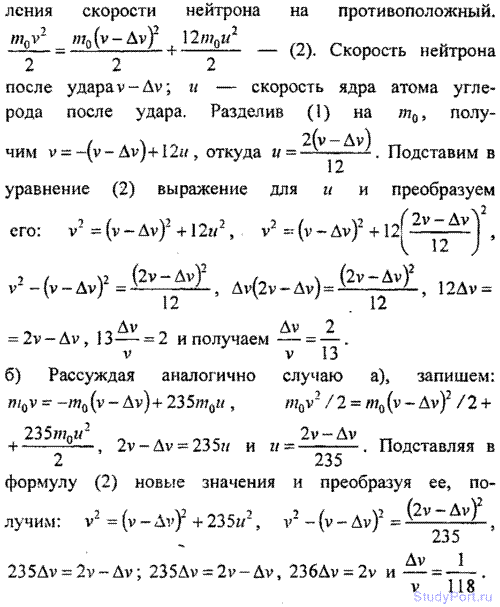
2.94. На какую часть уменьшится вес тела на экваторе вследствие вращения Земли вокруг оси?
Решение:
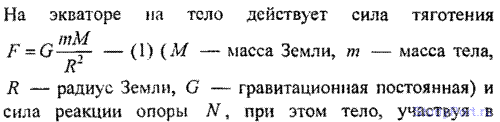

2.95. Какой продолжительности Т должны были бы быть сутки на Земле, чтобы тела на экваторе не имели веса.
Решение:
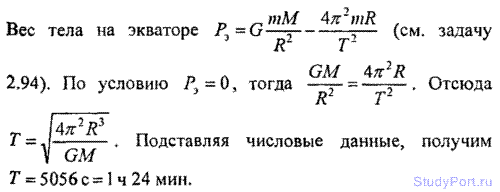
2.96. Трамвайный вагон массой т = 5 т идет по закруглению радиусом R = 128 м. Найти силу бокового давления F колес на рельсы при скорости движения v = 9 км/ч.
Решение:

2.97. Ведерко с водой, привязанное к веревке длиной l = 60 см,
равномерно вращается в вертикальной плоскости. Найти наименьшую
скорость v вращения ведерка, при которой в высшей точке вода из него не
выливается. Какова сила натя веревки Т при этой скорости в высшей и низшей точках окружности? Масса ведерка с водой m = 2 кг.
Решение:

2.98. Камень, привязанный к веревке длиной l = 50 см, равно вращается в вертикальной плоскости. При какой частоте вращения п веревка разорвется, если известно, что она разрыва при десятикратной силе тяжести, действующей на камень?
Решение:
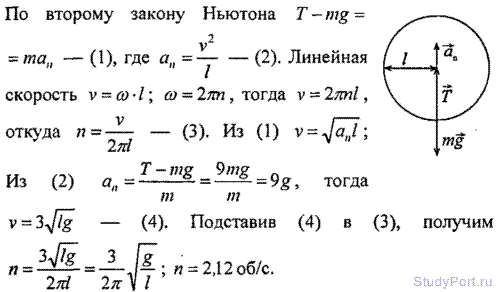
2.99. Камень, привязанный к веревке, равномерно вращается в вертикальной плоскости. Найти массу т камня, если известно, что разность между максимальной и минимальной силами натяжения веревки dT = 10 Н.
Решение:

2.100. Гирька, привязанная к нити длиной l = 30 см, описыва в горизонтальной плоскости окружность радиусом R = 15 см. С какой частотой п вращается гирька?
Решение:

2.101. Гирька массой т = 50 г, привязанная к нити длиной l = 25 см, описывает в горизонтальной плоскости окружность. Частота вращения гирьки п = 2 об/с. Найти силу натяжения нити Т.
Решение:
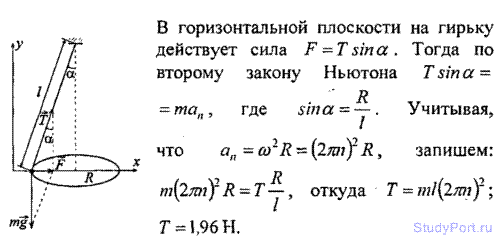
2.102. Диск вращается вокруг вертикальной оси с частотой п = 30 об/мин. На расстоянии r = 20 см от оси вращения на диске лежит тело. Каким должен быть коэффициент трения к между телом и диском, чтобы тело не скатилось с диска?
Решение:
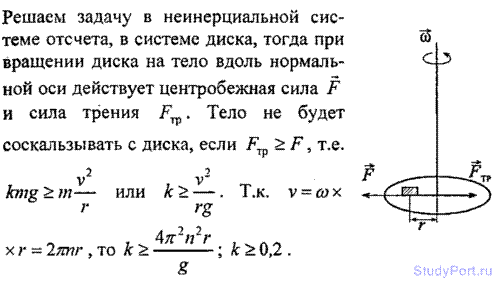
2.103. Самолет, летящий со скоростью v = 900 км/ч, делает «мертвую петлю». Каким должен быть радиус «мертвой петли» R, чтобы наибольшая сила F,
прижимающая летчика к сидению, была равна: а) пятикратной силе тяжести,
действу на летчика; б) десятикратной силе тяжести, действующей на
летчика?
Решение:
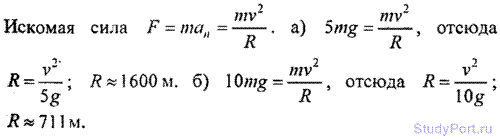
2.104. Мотоциклист едет по горизонтальной дороге со скоростью v = 72 км/ч, делая поворот радиусом R = 100 м. На какой угол а при этом он должен наклониться, чтобы не упасть при повороте?
Решение:

2.105. К потолку трамвайного вагона подвешен на нити шар. Вагон идет со скоростью v = 9 км/ч по закруглению радиусом R = 36,4 м. На какой угол а отклонится при этом нить с шаром?
Решение:
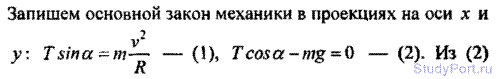
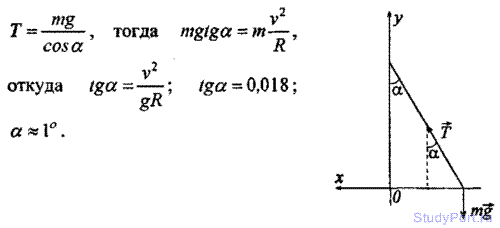
2.106. Длина стержней центробежного регулятора l = 12,5 см. С какой частотой п должен вращаться центробежный регулятор, чтобы грузы отклонялись от вертикали на угол, равный: а) а = 60°; б) а = 30°?
Решение:

2.107. Шоссе имеет вираж с уклоном а = 10° при радиусе за дороги R = 100 м. На какую скорость v рассчитан вираж?
Решение:

2.108. Груз массой т = 1 кг, подвешенный на нити, отклоня на угол а = 30° и отпускают. Найти силу натяжения нити Т в момент прохождения грузом положения равновесия.
Решение:

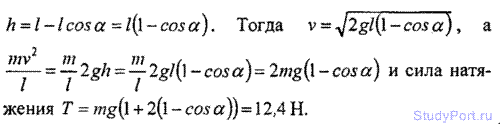
2.109. Мальчик массой т = 45 кг вращается на «гигантских шагах» с частотой n = 16 об/мин. Длина канатов / = 5м. Какой угол а с вертикалью составляют канаты «гигантских шагов»? Каковы сила натяжения канатов Т и скорость v вращения маль?
Решение:

2.110. Груз массой m = 1кг, подвешенный на невесомом стержне длиной l
= 0,5 м, совершает колебания в вертикальной плоскости. При каком угле
отклонения а стержня от вертикали кинетическая энергия груза в его нижнем положении WK = 2,45 Дж? Во сколько раз при таком угле отклонения сила натяжения стержня Т1 в нижнем положении больше силы натяжения стержня Тг в верхнем положении?
Решение:

2.111. Груз массой m, подвешенный на невесомом стержне, отклоняют на угол а = 90° и отпускают. Найти силу натяжения Т стержня в момент прохождения грузом положения равновесия.
Решение:

2.112. Груз массой т = 150 кг подвешен на стальной проволо, выдерживающей силу натяжения Т = 2,94 кН. На какой наи угол а можно отклонить проволоку с грузом, чтобы она не разорвалась при прохождении грузом положения равно?
Решение:
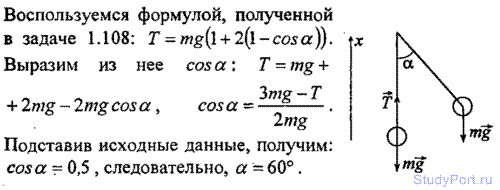
2.113. Камень массой m = 0,5 кг привязан к веревке длиной l = 50 см,
равномерно вращается в вертикальной плоскости. Сила натяжения веревки в
нижней точке окружности T = 44Н. На какую высоту h поднимется камень, если веревка обрывается в тот момент, когда скорость направлена вертикально вверх?
Решение:

2.114. Вода течет по трубе диаметром d = 0,2м, располо в горизонтальной плоскости и имеющей закругление радиусом R = 20,0 м. Найти боковое давление воды Р, вызван центробежной силой. Через поперечное сечение трубы за единицу времени протекает масса воды m1 = 300 т/ч.
Решение:

2.115. Вода течет по каналу шириной b = 0,5 м, располо в
горизонтальной плоскости и имеющему закругление радиусом R = 10м.
Скорость течения воды v = 5m/c. Найти боковое давление воды Р , вызванное центробежной силой.
Решение:

2.116. Найти работу А, которую надо совершить, чтобы сжать пружину на l = 20 см, если известно, что сила F пропор сжатию l и жесткость пружины k = 2,94 кН/м.
Решение:
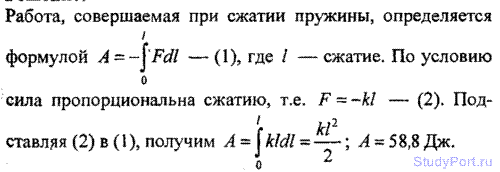
2.117. Найти наибольший прогиб h рессоры от груза массой m, положенного на ее середину, если статический прогиб рессоры от того же груза h0 = 2 см. Каким будет наибольший прогиб, если тот же груз падает на середину рессоры с высоты Н = 1 м без начальной скорости?
Решение:
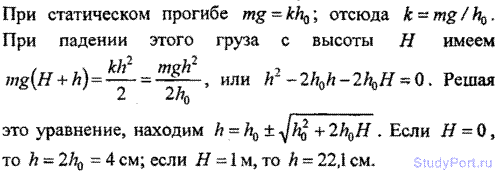
2.118. Акробат прыгает в сетку с высоты Я = 8м. На какой предельной высоте h над полом надо натянуть сетку, чтобы акробат не ударился о пол при прыжке? Известно, что сетка прогибается на hQ = 0,5 м, если акробат прыгает в нее с высоты H0 =1м.
Решение:

2.119. Груз положили на чашку весов. Сколько делений покажет стрелка
весов при первоначальном отбросе, если после успокоения качаний она
показывает 5 делений?
Решение:
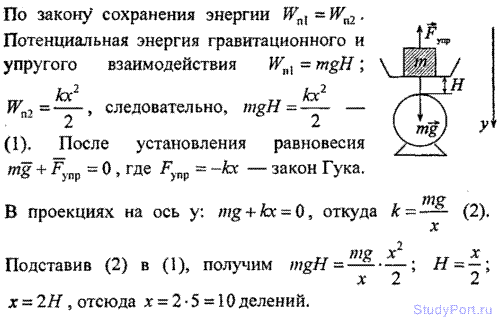
2.120. Груз массой т = 1 кг падает на чашку весов с высоты Н = 10 см. Каковы показания весов F в момент удара, если пос успокоения качаний чашка весов опускается на h = 0,5 см?
Решение:

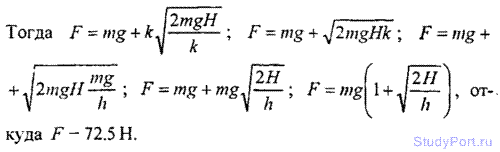
2.121. С какой скоростью v двигался вагон массой m = 20т, если при
ударе о стенку каждый буфер сжался на l = 10см? Жесткость пружины
каждого буфера к = 1 МН/м.
Решение:

2.122. Мальчик, стреляя из рогатки, натянул резиновый шнур так, что
его длина стала больше на dl = 10 см. С какой скоростью v полетел камень
массой т = 20 г? Жесткость шнура к = 1 кН/м.
Решение:

2.123. X нижнему концу пружины, подвешенной верти, присоединена
другая пружина, к концу которой прикреп груз. Жесткости пружин равны к1 и к2. Пренебрегая массой пружин по сравнению с массой груза, найти отношение Wn1 Wn2 потенциальных энергий этих пружин.
Решение:

2.124. На двух параллельных пружинах одинаковой длины весит невесомый стержень длиной L = 10 см. Жесткости пружин к1 - 2 Н/м и к2 = 3 Н/м. В каком месте стержня надо подвесить груз, чтобы стержень оставался горизонтальным?
Решение:


2.125. Резиновый мяч массой т = 0,1 кг летит горизонтально с некоторой скоростью и ударяется о неподвижную вертикальную стенку. За время dt = 0,01 с мяч сжимается на dl = 1,37 см; такое же время dt затрачивается на восстановление первоначальной формы мяча. Найти среднюю силу F , действующую на стенку за время удара.
Решение:
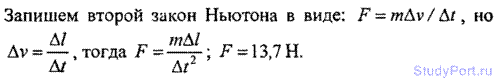
2.126. Гиря массой m = 0,5кг, привязанная к резиновому шнуру длиной l0, описывает в горизонтальной плоскости окружность. Частота вращения гири п = 2 об/с. Угол отклонения шнура от вертикали a=30°. Жесткость шнура к =0,6кН/м. Найти длину l0 нерастянутого резинового шнура.
Решение:

2.127. Гирю массой m = 0,5кг, привязанную к резиновому шнуру длиной l0 = 9,5 см, отклоняют на угол а = 90° и отпуска. Найти длину l резинового шнура в момент прохождения грузом положения равновесия. Жесткость шнура к = 1 кН/м.
Решение:

2.128. Мяч радиусом R = 10 см плавает в воде так, что
его центр масс находится на H = 9см выше поверхности воды. Какую работу
надо совершить, чтобы погрузить мяч в воду до диаметральной плоскости?
Решение:

2.129. Шар радиусом R = 6см удерживается внешней силой под водой так, что его верхняя точка касается поверхности воды. Какую работу А произведет выталкивающая сила, если отпустить
шар и предоставить ему свободно плавать? Плотность мате шара р = 0,5 • 103 кг/м3.
Решение:

2.130. Шар диаметром D = 30см плавает в воде. Какую работу А надо совершить, чтобы погрузить шар в воду на H = 5 см глубже? Плотность материала шара р = 0,5 • 103 кг/м3.
Решение:

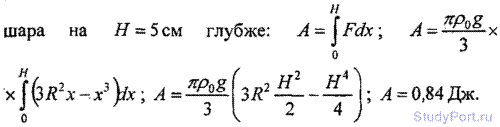
2.131. Льдина площадью поперечного сечения S = 1м2 и высотой h = 0,4 м плавает в воде. Какую работу А надо совершить, чтобы полностью погрузить льдину в воду?
Решение:

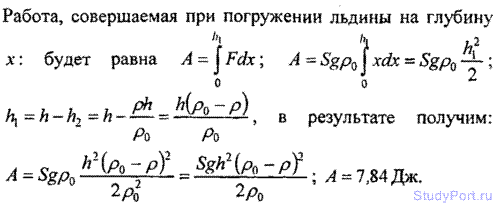
2.132. Найти силу гравитационного взаимодействия F между двумя протонами, находящимися на расстоянии r = 10-16м друг от друга. Масса протона т = 1,67-10-27 кг.
Решение:

2.133. Два медных шарика с диаметрами D1 =4 см и D2 = 6 см находятся в соприкосновении друг с другом. Найти гравитационную потенциальную энергию Wn этой системы.
Решение:

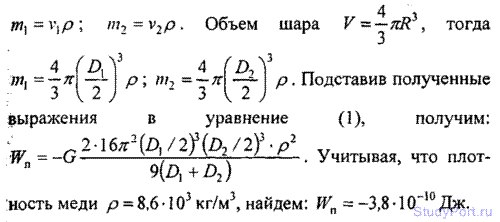
2.134. Вычислить гравитационную постоянную G, зная ра земного шара R , среднюю плотность земли р и ускорение свободного падения g у поверхности Земли (см. табл. 4 и 5).
Решение:

2.135. Принимая ускорение свободного падения у Земли g = 9,8 м/с2 и пользуясь данными табл. 5, составить таблицу значений средних плотностей планет Солнечной системы.
Решение:

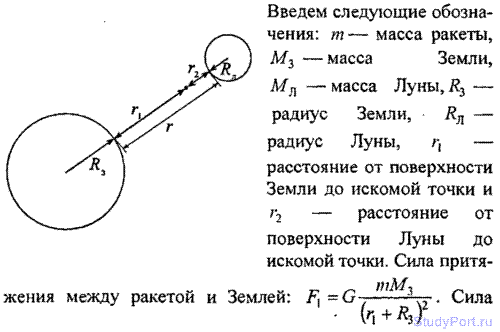
2.136. Космическая ракета летит на Луну. В какой точке прямой,
соединяющей центры масс Луны и Земли, ракета будет притягиваться Землей и
Луной с одинаковой силой?
Решение:

2.137. Сравнить ускорение свободного падения у поверхности Луны gЛ с ускорением свободного падения у поверхности Земли gЗ.
Решение:
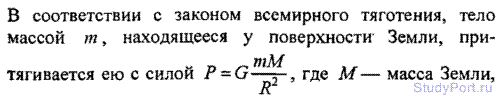
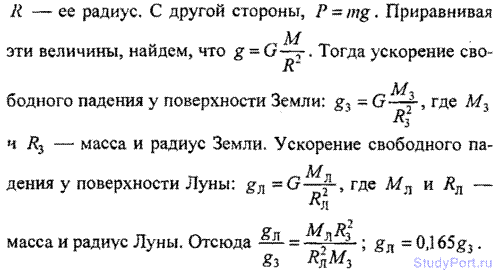
2.138. Как изменится период колебания Т математического
маятника при перенесении его с Земли на Луну? Указание: формула для
периода колебания математического маятника при в §12.
Решение:

2.139. Найти первую космическую скорость v1, т.е.
скорость, которую надо сообщить телу у поверхности Земли, чтобы оно
начало двигаться по круговой орбите в качестве ее спутника.
Решение:

2.140. Найти вторую космическую скорость v2, т.е.
скорость, которую надо сообщить телу у поверхности Земли, чтобы оно
преодолело земное тяготение и навсегда удалилось от Земли.
Решение:

2.141. Принимая ускорение свободного падения у Земли равным g = 9,80 м/с2
и пользуясь данными табл. 5, составить таблицу значений первой и второй
космических скоростей у поверхности планет Солнечной системы.
Решение:

2.142. Найти линейную скорость v движения Земли по круго орбите.
Решение:

2.143. С какой линейной скоростью v будет двигаться искусственный
спутник Земли по круговой орбите: а) у повер Земли; б) на высоте h = 200 км и h = 7000 км от поверх Земли? Найти период обращения Т спутника Земли при этих условиях.
Решение:
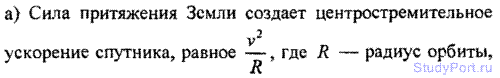

2.144. Найти зависимость периода обращения Т искус спутника,
вращающегося по круговой орбите у поверхности центрального тела, от
средней плотности этого тела. По данным, полученным при решении задачи
2.135, соста таблицу значений периодов обращений искусственных спутников
вокруг планет Солнечной системы.
Решение:

2.145. Найти центростремительное ускорение an, с которым движется по круговой орбите искусственный спутник Земли, находящийся на высоте h = 200 км от поверхности Земли.
Решение:

2.146. Планета Марс имеет два спутника — Фобос и Деймос. Первый находится на расстоянии r = 0,95-104 км от центра масс Марса, второй на расстоянии r = 2,4 • 104 км. Найти период обра T1 и Т2 этих спутников вокруг Марса.
Решение:

2.147. Искусственный спутник Земли движется по круговой орбите в плоскости экватора с запада на восток. На какой высоте h от
поверхности Земли должен находиться этот спутник, чтобы он был
неподвижен по отношению к наблюдателю, который находится на Земле?
Решение:

2.148. Искусственный спутник Луны движется по круговой орбите на высоте h = 20 км от поверхности Луны. Найти линейную скорость v движения этого спутника, а также период его обращения Т вокруг Луны.
Решение:
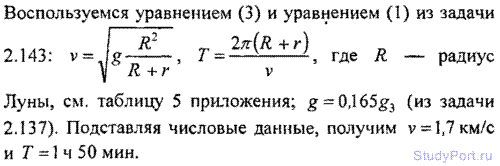
2.149. Найти первую и вторую космические скорости для Луны (см. условия 2.139 и 2.140).
Решение:

2.150. Найти зависимость ускорения свободного падения g от высоты h над поверхностью Земли. На какой высоте h ускорение свободного падения gh составит 0,25 ускорения свободного падения g у поверхности Земли.
Решение:
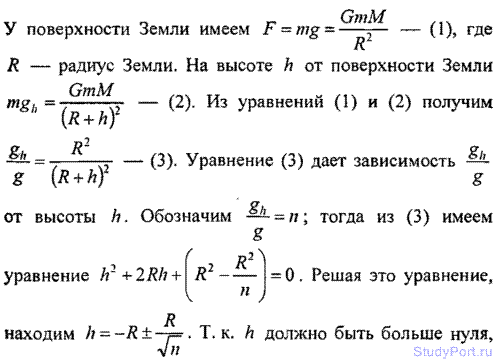
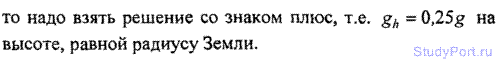
2.151. На какой высоте h от поверхности Земли ускорение свободного падения gh = 1 м/с2?
Решение:
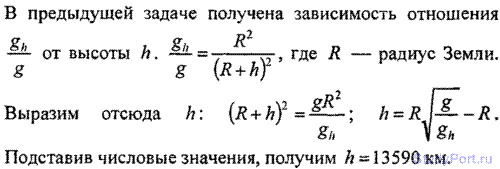
2.152. Во сколько раз кинетическая энергия WK искусствен спутника Земли, движущегося по круговой орбите, меньше его гравитационной потенциальной энергии Wn ?
Решение:

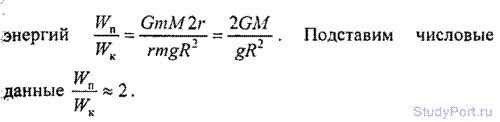
2.153. Найти изменение ускорения свободного падения при опускании тела на глубину h. На какой глубине ускорение свободного падения gh составляет
0,25 ускорения свободного падения g у поверхности Земли? Плотность
Земли считать постоянной. Указание: учесть, что тело, находящееся на
глуби h над поверхностью Земли, не испытывает со стороны вышележащего слоя толщиной h никакого притяжения, так как притяжения отдельных частей слоя взаимно компенсируются.
Решение:

2.154. Каково соотношение между высотой Н горы и глубиной h шахты,
если период колебания маятника на вершине горы и на дне шахты один и
тот же. Указание: формула для периода колебания математического маятника
приведена в § 12.
Решение:

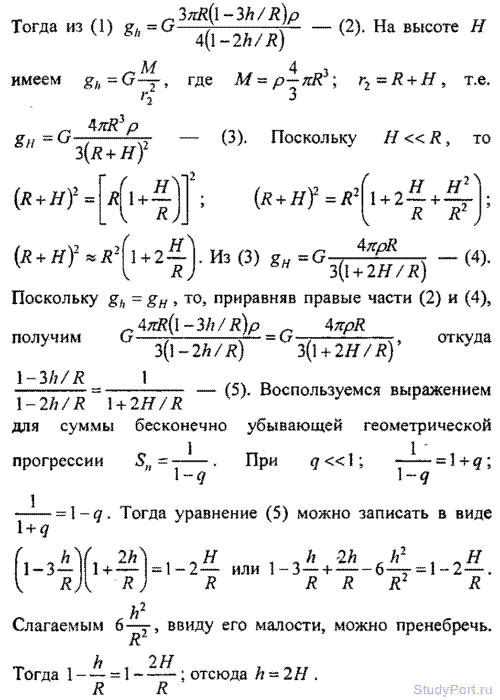
2.155. Найти период обращения Т вокруг Солнца искусственной планеты, если известно, что большая полуось R
2.155. Найти период обращения Т вокруг Солнца искусственной планеты, если известно, что большая полуось R1
2.155. Найти период обращения Т вокруг Солнца искусственной планеты, если известно, что большая полуось R1
ее эллиптической орбиты превышает большую полуось R2 земной орбиты на dR = 0,24 • 108 км.
Решение:

2.156. Орбита искусственной планеты близка к круговой. Найти линейную скорость v ее движения и период Т ее обращения вокруг Солнца, считая известным диаметр Солнца D и его среднюю плотность р. Среднее расстояние планеты от Солнца r = 1,71 • 108 км.
Решение:

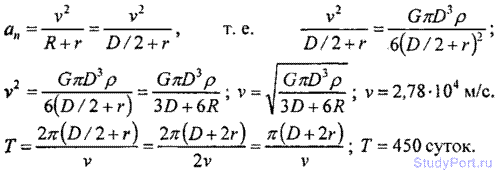
2.157. Большая полуось R1 эллиптической орбиты первого в мире спутника Земли меньше большой полуоси R2 орбиты вто спутника на dR = 800 км. Период обращения вокруг Земли первого спутника в начале его движения был T1 = 96,2 мин. Найти большую полуось R2 орбиты второго искусственного спутника Земли и период Т2 его обращения вокруг Земли.
Решение:

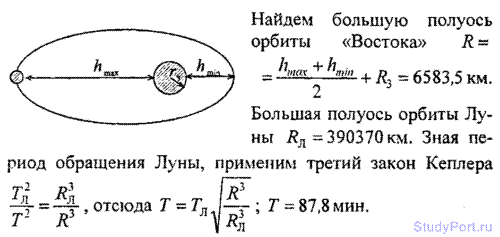
2.158. Минимальное удаление от поверхности Земли косми корабля-спутника «Восток-2» составляло hmln = 183 км, а максимальное удаление — hmax = 244 км. Найти период обра Т спутника вокруг Земли.
Решение:
2.159. Имеется кольцо радиусом R . Радиус проволоки равен r, плотность материала равна р . Найти силу F, с которой это кольцо притягивает материальную точку массой т, находящую на оси кольца на расстоянии L от его центра.
Решение:

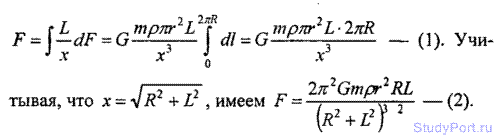
2.160. Имеется кольцо радиусом R = 20 см из медной проволоки. Найти силу F, с которой это кольцо притягивает материальную точку массой т = 2 г, находящуюся на оси кольца на расстоянии L = 0, 5, 10, 15, 20 и 50 см от его центра. Составить таблицу значений F и представить графически зависимость F = f(L). На каком расстоянии Lmax от центра кольца сила имеет максимальное значение Fmax и каково это значение? Радиус проволоки r = 1 мм.
Решение:
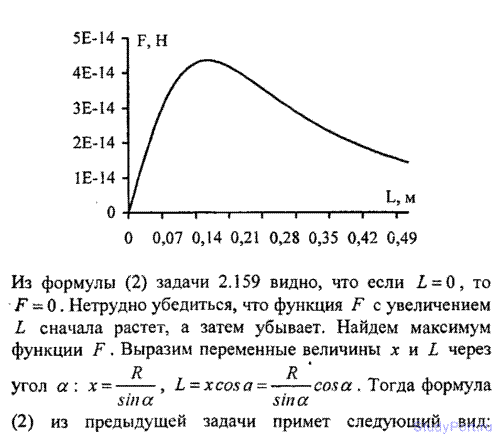

2.161. Сила взаимодействия между кольцом и материальной точкой, находящейся на оси кольца, имеет максимальное значение Fmax, когда точка находится на расстоянии Lтах от центра кольца. Во сколько раз сила взаимодействия F между кольцом и материальной точкой, находящейся на расстоянии L = 0,5Lmax от центра кольца, меньше максимальной силы Fmax ?
Решение:

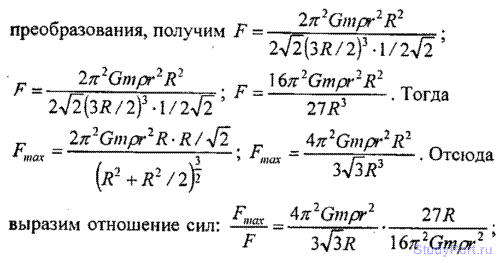

Источник http://studyport.ru/volkenshteyn/
|